早教吧作业答案频道 -->数学-->
如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.(1)求证:PE=PF(2)已知AG=4,AF=5,EF=25,求圆O的直径.
题目详情
如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
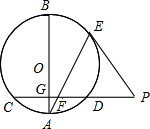
(1)求证:PE=PF
(2)已知AG=4,AF=5,EF=25,求圆O的直径.

(1)求证:PE=PF
(2)已知AG=4,AF=5,EF=25,求圆O的直径.
▼优质解答
答案和解析
(1)证明:如图1,连接OE,
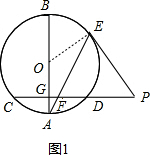
∵EP是 O的切线,
∴∠PEO=90°,
∴∠OEA+∠PEF=90°,
∵AB⊥CD,
∴∠AGF=90°,
∴∠A+∠AFG=90°,
∵OE=OA,
∴∠OEA=∠OAE,
∴∠PEF=∠AFG,
∵∠EFP=∠AFG,
∴∠PEF=∠PFE,
∴PE=PF;
(2) 如图2,连接BE,
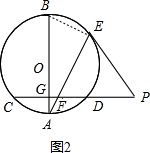
∵AB为直径,
∴∠AEB=90°,
∵∠AGF=90°,
∴∠AGF=∠AEB,
∵∠A=∠A,
∴△AGF∽△AEB,
∴
=
,
∵AG=4,AF=5,EF=25,
∴
=
,
∴AB=
,
即圆O的直径为
.

∵EP是 O的切线,
∴∠PEO=90°,
∴∠OEA+∠PEF=90°,
∵AB⊥CD,
∴∠AGF=90°,
∴∠A+∠AFG=90°,
∵OE=OA,
∴∠OEA=∠OAE,
∴∠PEF=∠AFG,
∵∠EFP=∠AFG,
∴∠PEF=∠PFE,
∴PE=PF;
(2) 如图2,连接BE,

∵AB为直径,
∴∠AEB=90°,
∵∠AGF=90°,
∴∠AGF=∠AEB,
∵∠A=∠A,
∴△AGF∽△AEB,
∴
| AG |
| AE |
| AF |
| AB |
∵AG=4,AF=5,EF=25,
∴
| 4 |
| 5+25 |
| 5 |
| AB |
∴AB=
| 75 |
| 2 |
即圆O的直径为
| 75 |
| 2 |
看了 如图,AB是圆O的一条直径,...的网友还看了以下:
如图,已知直线l:y=33x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y 2020-05-13 …
如图,已知直线l:y=√3/3x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线 2020-05-13 …
如图,已知直线l:y=3√3x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交 2020-05-17 …
如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A 2020-05-17 …
AB为圆O的直径,点C为圆O上的一点,AD和过点C的切线互相垂直,垂足为点D过点D作CE垂直于AB 2020-05-21 …
平面上的垂直必须相交吗直线不是可以无限延长的吗?既然这样,垂线也可以无限延长,直到相交,不是吗? 2020-06-15 …
如图,在△ABC中,AD是中线,O为AD上的中点,直线l过o点,过A,B,C三点分别作直线L的垂线 2020-06-22 …
(1/2)在三角形ABC中,AB=AC,AD垂直于BC,垂足为点D,AN是三角形ABC外角角CAM 2020-06-27 …
如图,正方体ABCD-A1B1C1D1的棱长为1,过点A作平面A1BD的垂线,垂足为H,则以下命题 2020-07-30 …
已知:如图,A,K是圆O上的两点,直线FN垂直于MA,垂足为N,FN与圆O相切与点F,角AOK=2角 2020-10-31 …