早教吧作业答案频道 -->数学-->
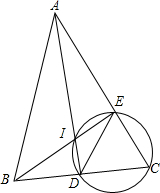
如图,若AD、BE为△ABC的两条角平分线,I为内心,若C,D,I,E四点共圆,且DE=1,则ID=.
题目详情
如图,若AD、BE为△ABC的两条角平分线,I为内心,若C,D,I,E四点共圆,且DE=1,则ID=___.

▼优质解答
答案和解析
连接CI,
∵AD、BE为△ABC的两条角平分线,
∴∠BAI=
∠BAC,∠IBA=
∠ABC,
∵∠AIB=180°-∠BAI-∠IBA,
∴∠AIB=180°-
(∠CAB+∠CBA),
又∵∠ABC+∠CBA+∠ACB=180°,
∴∠AIB=90°+
∠C,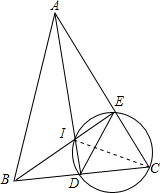
∵C,D,I,E四点共圆,
∴∠EID+∠ACB=180°,
又∵∠AIB=∠EID,
∴90°+
∠C+∠C=180°,
∴∠ACB=60°,
∵I为内心,
∴∠ICD=30°,
∵DE=1,
∴
=2R,
∴R=
,
∴
=2R,
∴ID=
,
故答案为:
.
∵AD、BE为△ABC的两条角平分线,
∴∠BAI=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AIB=180°-∠BAI-∠IBA,
∴∠AIB=180°-
| 1 |
| 2 |
又∵∠ABC+∠CBA+∠ACB=180°,
∴∠AIB=90°+
| 1 |
| 2 |

∵C,D,I,E四点共圆,
∴∠EID+∠ACB=180°,
又∵∠AIB=∠EID,
∴90°+
| 1 |
| 2 |
∴∠ACB=60°,
∵I为内心,
∴∠ICD=30°,
∵DE=1,
∴
| DE |
| sin60° |
∴R=
| ||
| 3 |
∴
| ID |
| sin30° |
∴ID=
| ||
| 3 |
故答案为:
| ||
| 3 |
看了 如图,若AD、BE为△ABC...的网友还看了以下:
设椭圆E:x²/a²+y²/1-a²=1的焦点在x轴上若椭圆E的焦距为1设椭圆E:x²/a²+设椭 2020-05-15 …
1若a,b,x,y属于正数,证明:x分之a平方+y分之b平方大于等于(x+y)分之(a+b)的平方 2020-06-02 …
第一题令A={a,b,c,d,e},B={a,b,c,d,e,f,g,h}.求a)A∪Bb)A∩B 2020-06-17 …
对于平行反应,A→P(主反应),A→S(副反应)主副反应均为二级不可逆反应,若E主>E副,为了提高 2020-06-17 …
设A,B均为n阶方阵,E为n阶单位阵,且(A-E)(B-E)=0A=E或B=E|A-E|=0或|B 2020-06-18 …
用以下英文宇母填在上a,a,a,a,a,a,b,e,e,d,e,e,e,e,e,e,f,g,g用以 2020-06-24 …
若E(e^aξ)<∞,试证P{ξ≥x}≤e^(-ax)*E(e^aξ)这是一道概率论的问题,需要用 2020-07-20 …
已知函数f(x)=(a+lnx)除以x(a属于R)若a=4求曲线F(X)在点(e,f(e)处的切线 2020-07-27 …
椭圆E:x2a2+y2b2=1(a>b>0)的左右焦点分别为F1,F2.(Ⅰ)若椭圆E的长轴长、短 2020-07-31 …
设函数f(x)=ex+x−a−−−−−−−−−√(a∈R,e为自然对数的底数),若曲线y=sinx 2020-08-02 …