如图，四边形ABCD是平行四边形，点E在BC的延长线上，且CE=BC，AE=AB，AE、DC相交于点O，连接DE．（1）求证：四边形ACED是矩形；（2）若∠AOD=120°，AC=4，求对角线CD的长．

Question

如图，四边形ABCD是平行四边形，点E在BC的延长线上，且CE=BC，AE=AB，AE、DC相交于点O，连接DE．

（1）求证：四边形ACED是矩形；

（2）若∠AOD=120°，AC=4，求对角线CD的长．

Answer 1

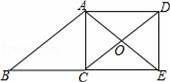
【考点】矩形的判定；平行四边形的性质．

【分析】（1）根据平行四边形的性质得出AD∥BC，AD=BC，AB=DC，求出AD=CE，AD∥CE，AE=DC，根据矩形的判定得出即可；

（2）根据矩形的性质得出OA=AE，OC=CD，AE=CD，求出OA=OC，求出△AOC是等边三角形，即可得出答案．

【解答】（1）证明：∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC，AB=DC，

∵CE=BC，

∴AD=CE，AD∥CE，

∴四边形ACED是平行四边形，

∵AB=DC，AE=AB，

∴AE=DC，

∴四边形ACED是矩形；

（2）∵四边形ACED是矩形，

∴OA=AE，OC=CD，AE=CD，

∴OA=OC，

∵∠AOC=180°﹣∠AOD=180°﹣120°=60°，

∴△AOC是等边三角形，

∴OC=AC=4，

∴CD=8．

【点评】本题考查了矩形的性质和判定，平行四边形的性质，等边三角形的性质和判定的应用，能综合运用定理进行推理是解此题的关键．