早教吧作业答案频道 -->数学-->
如图,等腰Rt△ABC中,∠ACB=90°,CA=CB,点D在AB上,AD=AC,BE⊥直线CD于E(1)求∠BCD的度数;(2)求证:CD=2BE;(3)若点O是AB的中点,请直接写出三条线段CB、BD、CO之间的数量关系.
题目详情
如图,等腰Rt△ABC中,∠ACB=90°,CA=CB,点D在AB上,AD=AC,BE⊥直线CD于E
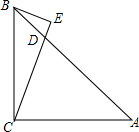
(1)求∠BCD的度数;
(2)求证:CD=2BE;
(3)若点O是AB的中点,请直接写出三条线段CB、BD、CO之间的数量关系.

(1)求∠BCD的度数;
(2)求证:CD=2BE;
(3)若点O是AB的中点,请直接写出三条线段CB、BD、CO之间的数量关系.
▼优质解答
答案和解析
(1)∵等腰Rt△ABC中,∠ACB=90°,CA=CB,
∴∠A=∠CBA=45°,
∵AD=AC,
∴∠ACD=67.5°,
∴∠BCD=90°-∠ACD=22.5°;
(2)作AH⊥CD于H,如图:
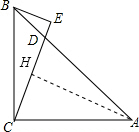
∵BE⊥直线CD于E,AC=AD,
∴CD=2CH,∠BEC=∠AHC=90°,
∵∠BCE+∠DCA=∠HAC+∠DCA=90°,
∴∠BCE=∠CAH,
在△CBE与△ACH中,
,
∴△CBE≌△ACH(AAS),
∴CH=BE,
即CD=2CH=2BE;
(3)如图,
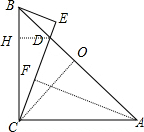
过D作DH⊥BC于点H,
由(1)可知∠BCD=22.5°,
∵O是AB的中点,
∴∠BCO=45°,
∴∠DCO=∠BCO=22.5°,
∴DO=DH,
在Rt△COD和Rt△CHD中,
,
∴Rt△COD≌Rt△CHD,
∴CH=CO,
∴∠DBH=45°,∠DHB=90°,
∴BH=
BD,
∴BC=CH+BH=CO+
BD.
∴∠A=∠CBA=45°,
∵AD=AC,
∴∠ACD=67.5°,
∴∠BCD=90°-∠ACD=22.5°;
(2)作AH⊥CD于H,如图:

∵BE⊥直线CD于E,AC=AD,
∴CD=2CH,∠BEC=∠AHC=90°,
∵∠BCE+∠DCA=∠HAC+∠DCA=90°,
∴∠BCE=∠CAH,
在△CBE与△ACH中,
|
∴△CBE≌△ACH(AAS),
∴CH=BE,
即CD=2CH=2BE;
(3)如图,

过D作DH⊥BC于点H,
由(1)可知∠BCD=22.5°,
∵O是AB的中点,
∴∠BCO=45°,
∴∠DCO=∠BCO=22.5°,
∴DO=DH,
在Rt△COD和Rt△CHD中,
|
∴Rt△COD≌Rt△CHD,
∴CH=CO,
∴∠DBH=45°,∠DHB=90°,
∴BH=
| ||
| 2 |
∴BC=CH+BH=CO+
| ||
| 2 |
看了 如图,等腰Rt△ABC中,∠...的网友还看了以下:
如图,已知AB‖CD,AD,BC相交于E,过点E作EF‖AB,交BD于点F,求证1/AB+1/AB 2020-04-26 …
如图,在平面直角坐标系xOy中,抛物线y=2mx2-2x与x轴负半轴交于点A,顶点为B,且对称轴与 2020-05-13 …
1、平行四边形ABCD中∠ABC的平分线交AD于E,且点E把AD分成5CM,6CM两部分,则四边形 2020-06-05 …
在三角形ABC中,角ACB=90度,CD垂直AB,角A的平分线交CD于F,交BC于E,过点E作EH 2020-06-06 …
如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E,交AB于E,点G是A 2020-06-15 …
聚点的概念是平面上p点的空心领域,但是既然聚点可以是边界点也可以是内点,为什么不就用p的领域而用空 2020-07-31 …
△ABC中,角C=90°,CD⊥AB于D,∠BAC的平方分线交CD于E,过点E作EF‖AB,交BC 2020-08-01 …
如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于D,交AB于 2020-08-03 …
在Rt△ABC中,∠ACB=90°,BC=30,AB=50,点P是AB边上任意一点,直线PE⊥AB, 2020-11-01 …
在Rt三角形ABC中,角ACB=90°,CA=CB,D为BC边的中点,DE垂直AB于E,过点B作BF 2020-12-01 …