早教吧作业答案频道 -->数学-->
如图,过O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交O于点E、F,过圆心O作OM⊥CD,垂足为M点.求证:(1)△ACO≌△BDO;(2)CE=DF.
题目详情
如图,过 O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交 O于点E、F,过圆心O作OM⊥CD,垂足为M点.
求证:(1)△ACO≌△BDO;(2)CE=DF.
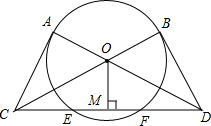
求证:(1)△ACO≌△BDO;(2)CE=DF.

▼优质解答
答案和解析
证明:(1)∵过 O上的两点A、B分别作切线,
∴∠CAO=∠DBO=90°,
在△ACO和△BDO中
∵
,
∴△ACO≌△BDO(ASA);
(2)∵△ACO≌△BDO,
∴CO=DO,
∵OM⊥CD,
∴MC=DM,EM=MF,
∴CE=DF.
∴∠CAO=∠DBO=90°,
在△ACO和△BDO中
∵
|
∴△ACO≌△BDO(ASA);
(2)∵△ACO≌△BDO,
∴CO=DO,
∵OM⊥CD,
∴MC=DM,EM=MF,
∴CE=DF.
看了 如图,过O上的两点A、B分别...的网友还看了以下:
已知圆o:x^2y^2=4和点M(1,a).若a=3,求过点M作圆O的切线的切线长已知圆o:x^2 2020-04-27 …
如图,已知圆O1,圆O2 外切于P,过圆O1上一点B作圆O1切线交圆O2于C、D,直线PB交圆O2 2020-05-17 …
过点a(5,2)和b(3,负二)圆心在直线2x-y=3上求圆的标准方程过点p(2,1)作圆x^2+ 2020-05-19 …
关于导数已知函数f(x)=x^3-3x及y=f(x)上一点P(1,-2),过点P作直线l1求使过直 2020-05-20 …
已知圆C:(x-1)平方+(y-2)平方=2,P点为(2,1),过点P作圆C的切线,切点为A.B. 2020-05-23 …
1.圆心在直线5X-3Y-8=0上的圆与两坐标轴相切,求此圆的方程2.已知圆C(X-1)的平方+( 2020-07-23 …
过点Q(-2,√21)作圆C:x^2+y^2=r^2(r>0)的切线,切点为D,且QD=4.(1) 2020-07-31 …
过点Q(-2,√21)作圆C:x^2+y^2=r^2(r>0)的切线,切点为D,且QD=4.求:设 2020-07-31 …
过点Q(−2,21)作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.(1)求r的值 2020-07-31 …
已知圆(x-2)²+(y-1)²=8和圆外一点M(4,8).(1)过M作圆的两条切线切点为C、D, 2020-07-31 …