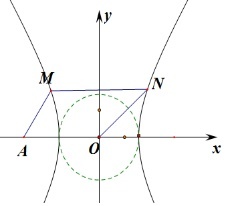
已知双曲线C：x2a2-y2b2=1（a>0，b>0）的左焦点为F（-c，0），M、N在双曲线C上，O是坐标原点，若四边形OFMN为平行四边形，且四边形OFMN的面积为2cb，则双曲线C的离心率为（）A.2B.2C.2

Question

已知双曲线C：

(x2)/(a2)-(y2)/(b2)=1（a>0，b>0）的左焦点为F（-c，0），M、N在双曲线C上，O是坐标原点，若四边形OFMN为平行四边形，且四边形OFMN的面积为√(2)cb，则双曲线C的离心率为（　　）

A.

√(2)

B. 2

C. 2

√(2)

D. 2

√(3)

Answer 1

双曲线C：(x2)/(a2)-(y2)/(b2)=1（a>0，b>0）焦点在x轴上，
设M（x₀，y₀），y₀>0，由四边形OFMN为平行四边形，
∴x₀=-(c)/(2)，
四边形OFMN的面积为√(2)cb，
∴丨y₀丨c=√(2)cb，即丨y₀丨=√(2)b，
∴M（-(c)/(2)，√(2)b），
代入双曲线可得：(x2)/(a2)-(y2)/(b2)=1，整理得：(c2)/(4a2)-2=1，
由e=(c)/(a)，
∴e²=12，由e>1，解得：e=2√(3)，
故选D．