抛物线y=ax2+bx+c交x轴于A（-1，0），B（3，0），交y轴的负半轴于C，顶点为D．下列结论：①2a+b=0；②2c<3b；③当m≠1时，a+b<am2+bm；④当△ABD是等腰直角三角形时，则a=12；⑤当△ABC是等腰三

Question

抛物线y=ax²+bx+c交x轴于A（-1，0），B（3，0），交y轴的负半轴于C，顶点为D．下列结论：
①2a+b=0；②2c<3b；③当m≠1时，a+b<am²+bm；④当△ABD是等腰直角三角形时，则a=

(1)/(2)；⑤当△ABC是等腰三角形时，a的值有3个．
其中正确的有（　　）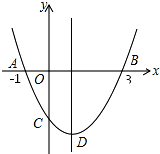

A. ①③④

B. ①②④

C. ①③⑤

D. ③④⑤

Answer 1

∵二次函数与x轴交于点A（-1，0）、B（3，0）．
∴二次函数的对称轴为x=((-1)+3)/(2)=1，即-(b)/(2a)=1．
∴b=-2a．
∴2a+b=0．（故①正确）
∵二次函数y=ax²+bx+c与x轴交于点A（-1，0）、B（3，0）．
∴a-b+c=0，9a+3b+c=0．
又∵b=-2a．
∴3b=-6a，a-（-2a）+c=0．
∴3b=-6a，2c=-6a．
∴2c=3b．（故②错误）
∵抛物线开口向上，对称轴是x=1．
∴x=1时，二次函数有最小值．
∴m≠1时，a+b+c<am²+bm+c．
即a+b<am²+bm．（故③正确）
∵AD=BD，AB=4，△ABD是等腰直角三角形．
∴AD²+BD²=4²．
解得，AD²=8．
设点D坐标为（1，y）．
则[1-（-1）]²+y²=AD²．
解得y=±2．
∵点D在x轴下方．
∴点D为（1，-2）．
∵二次函数的顶点D为（1，-2），过点A（-1，0）．
设二次函数解析式为y=a（x-1）²-2．
∴0=a（-1-1）²-2．
解得a=(1)/(2)．（故④正确）
由图象可得，AC≠BC．
故△ABC是等腰三角形时，a的值有2个．（故⑤错误）
故①③④正确，②⑤错误．
故选项A正确，选项B错误，选项C错误，选项D错误．
故选A．