早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=kx(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3(1)求反比例函
题目详情
如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3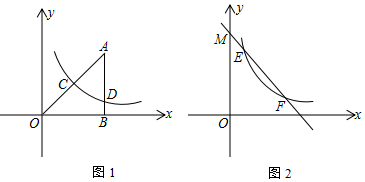
(1)求反比例函数y=
的解析式;
(2)若直线y=-x+m与反比例函数y=
(x>0)的图象相交于两个不同点E、F(点E在点F的左边),与y轴相交于点M
①则m的取值范围为___(请直接写出结果)
②求ME•MF的值.
| k |
| x |

(1)求反比例函数y=
| k |
| x |
(2)若直线y=-x+m与反比例函数y=
| k |
| x |
①则m的取值范围为___(请直接写出结果)
②求ME•MF的值.
▼优质解答
答案和解析
(1)设D的坐标是(4,a),则A的坐标是(4,a+3).
又∵点C是OA的中点,
∴点C的坐标是(2,
),
∴4a=2×
=k,
解得a=1,k=4,
∴反比例函数的解析式为y=
;
(2)①将y=-x+m代入y=
中,-x+m=
,
整理,得:x2-mx+4=0,
∵直线y=-x+m与反比例函数y=
(x>0)的图象相交于两个不同点E、F,
∴
,
解得:m>4.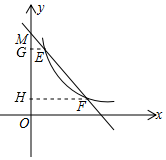
故答案为:m>4.
②过点E、F分别作y轴的垂线,垂足分别为G、H.
由y=-x+m可知:∠MEG=∠MFH=45°,
∴ME=
GE,MF=
HF.
由y=-x+m=
,得x2-mx+4=0,
∴xE•xF=4,
∴ME•MF=2xE•xF=8.
又∵点C是OA的中点,
∴点C的坐标是(2,
| a+3 |
| 2 |
∴4a=2×
| a+3 |
| 2 |
解得a=1,k=4,
∴反比例函数的解析式为y=
| 4 |
| x |
(2)①将y=-x+m代入y=
| 4 |
| x |
| 4 |
| x |
整理,得:x2-mx+4=0,
∵直线y=-x+m与反比例函数y=
| k |
| x |
∴
|
解得:m>4.

故答案为:m>4.
②过点E、F分别作y轴的垂线,垂足分别为G、H.
由y=-x+m可知:∠MEG=∠MFH=45°,
∴ME=
| 2 |
| 2 |
由y=-x+m=
| 4 |
| x |
∴xE•xF=4,
∴ME•MF=2xE•xF=8.
看了 如图,在平面直角坐标系中,O...的网友还看了以下:
如图,已知直线y=x+b与双曲线y=kx在第一象限内交于A点,交x轴于B点(B在O点左边).AC⊥ 2020-04-26 …
(2015•成都模拟)如图所示,电荷量Q=2×l0-7C的正点电荷A固定在空间中O点,将质量m=2 2020-06-12 …
如图所示,一不可伸长的轻绳一端固定于O点,绳的另一端系一质量为m的小球,光滑定滑轮B与O点等高.轻 2020-06-29 …
如图所示在一个固定的十字架上(横竖两杆连结点为O点),小球A套在竖直杆上,小球B套在水平杆上,A、 2020-07-19 …
如图4-21所示,质量为m的物体,沿半径为R的圆轨道自A点滑下(A与圆心O等高),滑至B点(B在O 2020-07-31 …
图中a、b是两个等量正点电荷,O点为a、b连线的中点,M、N是a、b连线的中垂线上的两点。下列判断 2020-08-01 …
如图所示,轻绳a、b将灯笼悬挂于O点.灯笼保持静止,所受重力为G,绳a、b对O点拉力的合力为F,F的 2020-11-30 …
如图所示,在y轴上关于O点对称的A、B两点有等量同种点电荷+Q,在x轴上有一点C,且CO=OD,∠A 2020-12-24 …
如图所示,电流从A点分两路对称地通过圆环形支路再汇合于B点,则对圆环中心处O点的磁感应强度的描述正确 2021-01-13 …
如图所示,光滑圆弧形轨道半径R=10m,一小球A自最低点O开始在槽内做往复运动,当A开始运动时,离O 2021-01-14 …