早教吧作业答案频道 -->数学-->
如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C.(1)若△ABC为直角三角形,求a•c的值;(2)在a=1的条件下,①若b=-2,c=-3,点D为抛物线上的动点,求满足△ABD为直
题目详情
如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C.
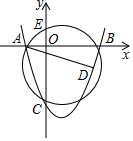
(1)若△ABC为直角三角形,求a•c的值;
(2)在a=1的条件下,
①若b=-2,c=-3,点D为抛物线上的动点,求满足△ABD为直角三角形的点D的坐标.
②若过点A、B、C三点的圆交y轴于另一点E,证明:不论b,c取何值,点E为定点.
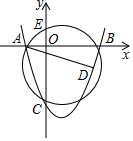
(1)若△ABC为直角三角形,求a•c的值;
(2)在a=1的条件下,
①若b=-2,c=-3,点D为抛物线上的动点,求满足△ABD为直角三角形的点D的坐标.
②若过点A、B、C三点的圆交y轴于另一点E,证明:不论b,c取何值,点E为定点.
▼优质解答
答案和解析
(1) 如图1中,设A(x1,0),B(x2,0),
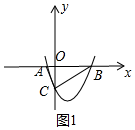
∵△ABC是直角三角形,
∴∠ACB=90°,
∵∠ACO+∠CAO=90°,∠CAB+∠CBO=90°,
∴∠ACO=∠CBO,∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴
=
,
∴OC2=OA•OB,
∵OC=-c,OA•OB=-x1•x2,x1x2=
,
∴c2=-x1x1,
∴c2=-
,
∴ac=-1.
(2)①如图2中,设AB的中点为K(1,0),D(m,m2-2m-3).
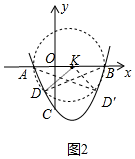
由题意KD=2,
∴(m-1)2+(m2-2m-3)2=4,
∴m2-2m+1+(m2-2m-3)2=4,
∴m2-2m-3+(m2-2m-3)2=0,
∴(m2-2m-3)(1+m2-2m-3)=0,
∴m2-2m-3=0或m2-2m-2=0,
解得m=1+
或1-
或-1或3,(m=-1或m=3不合题意舍弃)
∴D(1-
,-1),D′(1+
,-1).
②证明:如答图3,连接AD、BC.
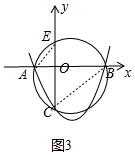
∵∠ADO=∠CBO,∠DAO=∠BCO,
∴△AOE∽△COB,
∴
=
,
设A(x1,0),B(x2,0),
∵已知抛物线y=x2+bx+c(c<0),∴OC=-c,x1x2=c.
∴
=
,
∴OE=
=
=1
∴无论b,c取何值,点E均为定点,该定点坐标E(0,1).

∵△ABC是直角三角形,
∴∠ACB=90°,
∵∠ACO+∠CAO=90°,∠CAB+∠CBO=90°,
∴∠ACO=∠CBO,∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴
| OA |
| CO |
| CO |
| OB |
∴OC2=OA•OB,
∵OC=-c,OA•OB=-x1•x2,x1x2=
| c |
| a |
∴c2=-x1x1,
∴c2=-
| c |
| a |
∴ac=-1.
(2)①如图2中,设AB的中点为K(1,0),D(m,m2-2m-3).
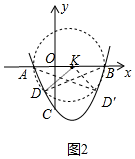
由题意KD=2,
∴(m-1)2+(m2-2m-3)2=4,
∴m2-2m+1+(m2-2m-3)2=4,
∴m2-2m-3+(m2-2m-3)2=0,
∴(m2-2m-3)(1+m2-2m-3)=0,
∴m2-2m-3=0或m2-2m-2=0,
解得m=1+
| 3 |
| 3 |
∴D(1-
| 3 |
| 3 |
②证明:如答图3,连接AD、BC.

∵∠ADO=∠CBO,∠DAO=∠BCO,
∴△AOE∽△COB,
∴
| OE |
| OB |
| OA |
| OC |
设A(x1,0),B(x2,0),
∵已知抛物线y=x2+bx+c(c<0),∴OC=-c,x1x2=c.
∴
| OE |
| x2 |
| x1 |
| -c |
∴OE=
| -x1x2 |
| -c |
| -c |
| -c |
∴无论b,c取何值,点E均为定点,该定点坐标E(0,1).
看了 如图,已知抛物线y=ax2+...的网友还看了以下:
一个数学压轴题最后一问,-只求第三问如图,在平面直角坐标系中,已知点A(-3,6),点B,点C分别在 2020-03-31 …
已知点A(3,4),B(-2.m)在反比例函数Y=K/X的图像上,经过点A、B的一次函数的图像分别 2020-04-08 …
一.用30平方米的草皮铺一块变长为10米的等腰三角形.请求出这个等腰三角形绿地的另两边边长.二.Y 2020-04-25 …
平面向量数量积的求解三角形ABC中,AC=2,BC=6,已知点O是三角形ABC内一点,且满足OA+ 2020-05-14 …
二次函数与一元二次方程.1、抛物线y=x^+3x+2交X轴于A、B交y轴于C,顶点是P,求S三角形 2020-05-16 …
如图,在平面直角坐标系中,三角形ABO为等边三角形,OA=6,D是y轴正半轴上的一点,且OD=6( 2020-05-17 …
一块地共x亩,计划三天耕完,拖拉机第一天耕了这块地的,第二天耕了剩下的,求第三天耕多少亩? 2020-05-22 …
急!求初三一道数学题两小时内要解答如图(图上的大致内容是:A在X轴负半轴,B在X轴正半轴,C在Y轴 2020-06-06 …
如图,椭圆C1:x2a2+y2b2=1(a>b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C 2020-06-21 …
急求助高人: 有xyz轴三个坐标,excel怎么画空间离散点图已经知道每个点的三个坐标 例如a( 2020-06-27 …