早教吧作业答案频道 -->数学-->
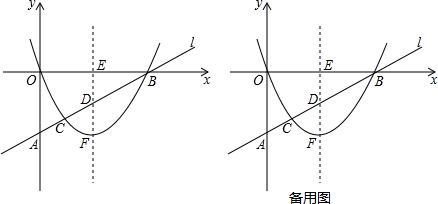
如图,已知:在平面直角坐标系中,直线l与y轴相交于点A(0,m)其中m<0,与x轴相交于点B(4,0).抛物线y=ax2+bx(a>0)的顶点为F,它与直线l相交于点C,其对称轴分别与直线l和x轴相交
题目详情
如图,已知:在平面直角坐标系中,直线l与y轴相交于点A(0,m)其中m<0,与x轴相交于点B(4,0).抛物线y=ax2+bx(a>0)的顶点为F,它与直线l相交于点C,其对称轴分别与直线l和x轴相交于点D和点E.
(1)设a=
,m=-2时,
①求出点C、点D的坐标;
②抛物线y=ax2+bx上是否存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形?如果存在,求出点G的坐标;如果不存在,请说明理由.
(2)当以F、C、D为顶点的三角形与△BED相似且满足三角形FAC的面积与三角形FBC面积之比为1:3时,求抛物线的函数表达式.
(1)设a=
| 1 |
| 2 |
①求出点C、点D的坐标;
②抛物线y=ax2+bx上是否存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形?如果存在,求出点G的坐标;如果不存在,请说明理由.
(2)当以F、C、D为顶点的三角形与△BED相似且满足三角形FAC的面积与三角形FBC面积之比为1:3时,求抛物线的函数表达式.

▼优质解答
答案和解析
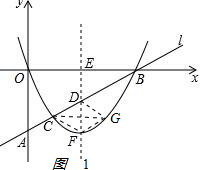
(1)①如图1,
 ,
,
当a=
时,将B点坐标代入,得y=
x2-2x=
(x-2)2-2顶点坐标为(2,-2);
当m=-2时,一次函数的解析式为y=
x-2.
联立抛物线与直线,得
2-2x=
x-2,
解得x=1,当x=1时,y=-
,即C点坐标为(1,-
).
当x=2时,y=-1,即D点坐标为(2,-1);
②假设存在g点,使得以G、C、D、F四点为顶点的四边形是平行四边形.
则CG与DF互相平分,而EF是抛物线的对称轴,且点G在抛物线上,
∴CG⊥DF,
∴DCFG是菱形,
∴点C关于EF的对称点G(3,-
).
设DF与CG与DF相交于O′点,则DO′=O′F=
,CO′=O′G=1,
∴四边形DCFG是平行四边形.
∴抛物线y=ax2+bx上存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形,点G的坐标为(3,-
);
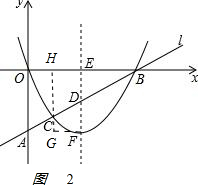
(2)如图2,
 ,
,
∵抛物线y=ax2+bx的图象过(4,0)点,16a+4b=0,
∴b=-4a.
∴y=ax2+bx=ax2-4ax=a(x-2)2-4a的对称轴是x=2,
∴F点坐标为(2,-4a).
∵三角形FAC的面积与三角形FBC面积之比为1:3,
BC:AC=3:1.
过点C作CH⊥OB于H,过点F作FG∥OB,FG与HC交于G点.
则四边形FGHE是矩形.
由HC∥OA,得BC:AC=3:1.
由HB:OH=3:1,OB=4,OE=EB,得
HE=1,HB=3.
将C点横坐标代入y=ax2-4ax,得y=-3a.
∴C(1,-3a),∴HC=3a,又F(2,-4a).
∴GH=4a,GC=a.
在△BED中,∠BED=90°,若△FCD与△BED相似,则△FCD是直角三角形.∵∠FDC=∠BDE<90°,∠CFD<90°,∴∠FCD=90°.
∴△BHC∽△CGF,
∴
=
,
∴
=
,
∴a2=1,
∴a=±1.
∵a>0,
∴a=1.
∴抛物线的解析式为y=x2-4x.
 ,
,当a=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当m=-2时,一次函数的解析式为y=
| 1 |
| 2 |
联立抛物线与直线,得
| 1 |
| 2 |
| 1 |
| 2 |
解得x=1,当x=1时,y=-
| 3 |
| 2 |
| 3 |
| 2 |
当x=2时,y=-1,即D点坐标为(2,-1);
②假设存在g点,使得以G、C、D、F四点为顶点的四边形是平行四边形.
则CG与DF互相平分,而EF是抛物线的对称轴,且点G在抛物线上,
∴CG⊥DF,
∴DCFG是菱形,
∴点C关于EF的对称点G(3,-
| 3 |
| 2 |
设DF与CG与DF相交于O′点,则DO′=O′F=
| 1 |
| 2 |
∴四边形DCFG是平行四边形.
∴抛物线y=ax2+bx上存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形,点G的坐标为(3,-
| 3 |
| 2 |
(2)如图2,
 ,
,∵抛物线y=ax2+bx的图象过(4,0)点,16a+4b=0,
∴b=-4a.
∴y=ax2+bx=ax2-4ax=a(x-2)2-4a的对称轴是x=2,
∴F点坐标为(2,-4a).
∵三角形FAC的面积与三角形FBC面积之比为1:3,
BC:AC=3:1.
过点C作CH⊥OB于H,过点F作FG∥OB,FG与HC交于G点.
则四边形FGHE是矩形.
由HC∥OA,得BC:AC=3:1.
由HB:OH=3:1,OB=4,OE=EB,得
HE=1,HB=3.
将C点横坐标代入y=ax2-4ax,得y=-3a.
∴C(1,-3a),∴HC=3a,又F(2,-4a).
∴GH=4a,GC=a.
在△BED中,∠BED=90°,若△FCD与△BED相似,则△FCD是直角三角形.∵∠FDC=∠BDE<90°,∠CFD<90°,∴∠FCD=90°.
∴△BHC∽△CGF,
∴
| BH |
| CG |
| HC |
| GF |
∴
| 3 |
| a |
| 3a |
| 1 |
∴a2=1,
∴a=±1.
∵a>0,
∴a=1.
∴抛物线的解析式为y=x2-4x.
看了 如图,已知:在平面直角坐标系...的网友还看了以下:
如图,直线l1:y=x+3与x轴交与点A,与y轴交于点P,直线l2:y=-2x+m与x轴交于点B, 2020-04-26 …
求解一个圆周运动的疑问假如让一个物体在转台上做由静止圆周运动,那么物体所受的摩擦力提供向心力,摩擦 2020-06-02 …
(2012•金东区一模)已知:如图,直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0, 2020-06-12 …
抛物线y=x^2-2x-3与x轴交与A,B两点,与y轴交与C点.设直线y=-x+3与y轴的交点抛物 2020-06-14 …
已知直线y=2x+6与x轴y轴交于A、B两点,直线L经过原点与线段AB交于点C,把△ABO的面积分 2020-06-23 …
过B0(0,1)作x轴的平行线,与直线y=2x相交于A1...急过B0(0,1)作x轴的平行线,与 2020-07-09 …
过点a(3,1)的直线与x轴的夹角为135度与y轴的正半轴交与点b直线ac交y轴与点c点c在点b方 2020-08-02 …
如图,已知在平面直角坐标系内直线y=-3/4x+3分别与x轴、y轴相交于点A和点B,直线m为过点O的 2020-12-25 …
如图,已知在平面直角坐标系内直线y=-3/4x+3分别与x轴、y轴相交于点A和点B,直线m为过点O的 2020-12-25 …
如图,已知在平面直角坐标系内直线y=-3/4x+3分别与x轴、y轴相交于点A和点B,直线m为过点O的 2020-12-25 …