早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.(1)求点A,B的坐标;(2)点C,D在x轴上(点C在点D的左侧),且与点B的距离都为2,若该抛物线与
题目详情
在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
(1)求点A,B的坐标;
(2)点C,D在x轴上(点C在点D的左侧),且与点B的距离都为2,若该抛物线与线段CD有两个公共点,结合函数的图象,求m的取值范围.
(1)求点A,B的坐标;
(2)点C,D在x轴上(点C在点D的左侧),且与点B的距离都为2,若该抛物线与线段CD有两个公共点,结合函数的图象,求m的取值范围.
▼优质解答
答案和解析
(1)由题意,当x=0时,y=2.
∴A(0,2).
∵y=mx2-2mx+2=m(x-1)2+2-m,
∴对称轴为直线x=1.
∴B(1,0).
(2)由题意,C(-1,0),D(3,0).
①当m>0时,
结合函数图象可知,满足题意的抛物线的顶点须在x轴下方,
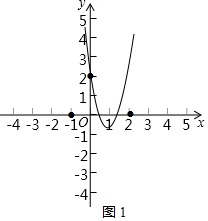
即2-m<0.
∴m>2.
②当m<0时,
过C(-1,0)的抛物线的顶点为E(1,
).
结合函数图象可知,满足条件的抛物线的顶点须在点E上方或与点E重合,
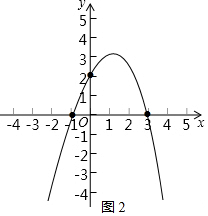
即2-m≥
.
∴m≤-
.
综上所述,m的取值范围为m>2或m≤-
.
∴A(0,2).
∵y=mx2-2mx+2=m(x-1)2+2-m,
∴对称轴为直线x=1.
∴B(1,0).
(2)由题意,C(-1,0),D(3,0).
①当m>0时,
结合函数图象可知,满足题意的抛物线的顶点须在x轴下方,

即2-m<0.
∴m>2.
②当m<0时,
过C(-1,0)的抛物线的顶点为E(1,
| 8 |
| 3 |
结合函数图象可知,满足条件的抛物线的顶点须在点E上方或与点E重合,

即2-m≥
| 8 |
| 3 |
∴m≤-
| 2 |
| 3 |
综上所述,m的取值范围为m>2或m≤-
| 2 |
| 3 |
看了 在平面直角坐标系xOy中,抛...的网友还看了以下:
已知平面α与平面β相交,直线m⊥α,则()A.β内必存在直线与m平行,且存在直线与m垂直B.β内不 2020-05-24 …
解一元二次方程,x的平方加2mx加4减m的平方是一个完全平方试,求m的至值.2(x减3)的平方等于 2020-06-19 …
抛物线y等于括号m减四括号x平方减2mx柬m减六的顶点在x轴上则m等于 2020-06-29 …
如果y=x的平方加2mx加(m的平方加m加3)有两个零点,则m的取值为? 2020-07-13 …
方程x的平方-2mx+m的平方-4=1的2根介于-2和3之间,则实数M的取值范围为什么?答案我已经 2020-07-30 …
平面α外有两条直线m和n,如果m和n在平面α内的射影分别是m′和n′,给出下列四个命题:①m′⊥n 2020-07-30 …
平面a外有两条直线m和n,如果m和n在平面a内的射影分别是m1和n1,给出下列四个命题:①m1⊥n 2020-07-30 …
y^2=2mx,z^2=m-x在点1,-2,1处的切线和法平面令Y^2=2mtZ^2=m-tx=t, 2020-11-01 …
不正确的命题(1816:26:49)1、平面A外两条直线m和n在平面内A的射影分别为m’和n’,给出 2020-11-14 …
高一数学问题已知函数y=根号下mx^(^是平方)-2mx+m+8的定义域是R求实数m的取值范围需要解 2020-12-18 …