早教吧作业答案频道 -->数学-->
如图,△ABC内接于O,过点B作O的切线DE,F为射线BD上一点,连接CF.(1)求证:∠CBE=∠A;(2)若O的直径为5,BF=2,tanA=2,求CF的长.
题目详情
如图,△ABC内接于 O,过点B作 O的切线DE,F为射线BD上一点,连接CF.
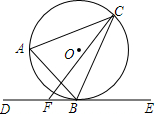
(1)求证:∠CBE=∠A;
(2)若 O的直径为5,BF=2,tanA=2,求CF的长.

(1)求证:∠CBE=∠A;
(2)若 O的直径为5,BF=2,tanA=2,求CF的长.
▼优质解答
答案和解析
(1)证明:如图,连接BO并延长交 O于点M,连接MC,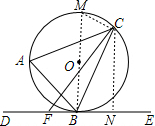
∴∠A=∠M,∠MCB=90°,
∴∠M+∠MBC=90°,
∵DE是 O的切线,
∴∠CBE+∠MBC=90°,
∴∠CBE=∠M,
∴∠CBE=∠A;
(2) 过点C作CN⊥DE于点N,
∴∠CNF=90°,
由(1)得,∠M=∠CBE=∠A,
∴tanM=tan∠CBE=tanA=2,
在Rt△BCM中,
∵BM=5,tanM=2,
∴BC=2
,
在Rt△CNB中,
∵BC=2
,tan∠CBE=2,
∴CN=4,BN=2,
∵BF=2,
∴FN=BF+BN=4,
在Rt△FNC中,
∵FN=4,CN=4,
∴CF=4
.

∴∠A=∠M,∠MCB=90°,
∴∠M+∠MBC=90°,
∵DE是 O的切线,
∴∠CBE+∠MBC=90°,
∴∠CBE=∠M,
∴∠CBE=∠A;
(2) 过点C作CN⊥DE于点N,
∴∠CNF=90°,
由(1)得,∠M=∠CBE=∠A,
∴tanM=tan∠CBE=tanA=2,
在Rt△BCM中,
∵BM=5,tanM=2,
∴BC=2
| 5 |
在Rt△CNB中,
∵BC=2
| 5 |
∴CN=4,BN=2,
∵BF=2,
∴FN=BF+BN=4,
在Rt△FNC中,
∵FN=4,CN=4,
∴CF=4
| 2 |
看了 如图,△ABC内接于O,过点...的网友还看了以下:
AB为圆O的直径点C为圆O上一点AD和过点C的切线互相垂直垂足为点D过点C作CE垂直AB垂足为点E直 2020-03-30 …
如图,AC为圆O的直径,△ABD为圆O的内接三角形,AB=BD,BD交AC于F点,BE//AD交A 2020-04-27 …
在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE垂直BC,垂足为E,连结DE交AC于点P 2020-05-16 …
如图,AB为圆O的直径,PB为O的切线,AC//OP,点C在圆O上,OP交圆O于D,DA交BC于G 2020-06-27 …
AB为圆O的直径,CD为圆0的玄且与AB垂直,E为AB上的任意一点,连接C.E与圆O交与F连接D. 2020-07-02 …
如图,AB为圆O的直径,CD为弦,且CD垂直AB,垂足为点H(1)角OCD的平分线CE交圆O于点E 2020-07-12 …
在圆O中,AB和CD是圆O的两条直径,且角AOC是60度,点P是弧AD上的一点,过点P作PE垂直A 2020-07-20 …
如图,四边形ABCD内接于圆O,AB为圆O的直径BC=CD,CE⊥如图,四边形ABCD内接于圆O, 2020-08-03 …
如图,AC为圆O的直径,三角形ABD为圆O的内接三角形,AB=BD,BD交AC于FBE平行于AD交 2020-08-03 …
(2012•菏泽二模)如图,EOF和E′O′F′为空间一匀强磁场的边界,其中EO∥E′O′,FO∥F 2020-11-13 …