早教吧作业答案频道 -->数学-->
已知如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β(1)如图1,若α+β=150°,求∠MBC+∠NDC的度数;(2)如图1,若BE与DF相交于点G,∠BGD=45°,请写出α、β所
题目详情
已知如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β
(1)如图1,若α+β=150°,求∠MBC+∠NDC的度数;
(2)如图1,若BE与DF相交于点G,∠BGD=45°,请写出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
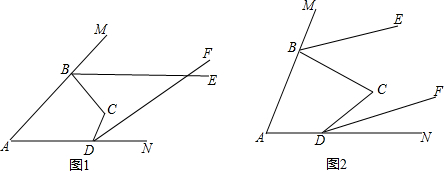
(1)如图1,若α+β=150°,求∠MBC+∠NDC的度数;
(2)如图1,若BE与DF相交于点G,∠BGD=45°,请写出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
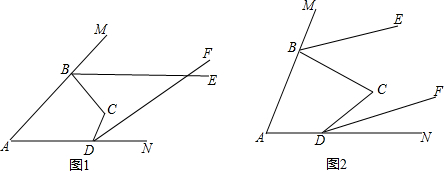
▼优质解答
答案和解析
(1)在四边形ABCD中,∠BAD+∠ABC+∠BCD+∠ADC=360°,
∴∠ABC+∠ADC=360°-(α+β),
∵∠MBC+∠ABC=180°,∠NDC+∠ADC=180°
∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC=360°-(∠ABC+∠ADC)=360°-[360°-(α+β)]=α+β,
∵α+β=150°,
∴∠MBC+∠NDC=150°,
(2)β-α=90°
理由:如图1,连接BD,
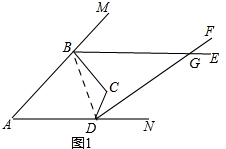
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=
∠MBC,∠CDG=
∠NDC,
∴∠CBG+∠CDG=
∠MBC+
∠NDC=
(∠MBC+∠NDC)=
(α+β),
在△BCD中,∠BDC+∠CDB=180°-∠BCD=180°-β,
在△BDG中,∠BGD=45°,
∴∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CDB)+∠BGD=180°,
∴
(α+β)+180°-β+45°=180°,
∴β-α=90°,
(3)平行,
理由:如图2,延长BC交DF于H,
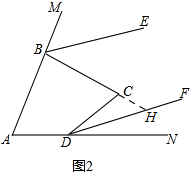
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=
∠MBC,∠CDH=
∠NDC,
∴∠CBE+∠CDH=
∠MBC+
∠NDC=
(∠MBC+∠NDC)=
(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD-∠DHB=β-∠DHB,
∴∠CBE+β-∠DHB=
(α+β),
∵α=β,
∴∠CBE+β-∠DHB=
(β+β)=β,
∴∠CBE=∠DHB,
∴BE∥DF.
∴∠ABC+∠ADC=360°-(α+β),
∵∠MBC+∠ABC=180°,∠NDC+∠ADC=180°
∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC=360°-(∠ABC+∠ADC)=360°-[360°-(α+β)]=α+β,
∵α+β=150°,
∴∠MBC+∠NDC=150°,
(2)β-α=90°
理由:如图1,连接BD,

由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CBG+∠CDG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在△BCD中,∠BDC+∠CDB=180°-∠BCD=180°-β,
在△BDG中,∠BGD=45°,
∴∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CDB)+∠BGD=180°,
∴
| 1 |
| 2 |
∴β-α=90°,
(3)平行,
理由:如图2,延长BC交DF于H,

由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CBE+∠CDH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD-∠DHB=β-∠DHB,
∴∠CBE+β-∠DHB=
| 1 |
| 2 |
∵α=β,
∴∠CBE+β-∠DHB=
| 1 |
| 2 |
∴∠CBE=∠DHB,
∴BE∥DF.
看了 已知如图,四边形ABCD,B...的网友还看了以下:
三角形ABC所对的边为abc,tanC=(sinA+sinB)÷(cosA+cosB),sin(B 2020-04-27 …
如图,在直角坐标系中,M为X轴上一点,⊙M交X轴于A,B两点,交Y轴于C,D两点,P为BC弧上的一 2020-05-16 …
已知圆C:x^2+y^2+2x-6y+1=0,直线l:x+my=31 若l与C相切,求M的值2 是 2020-06-27 …
.已知点A(5,0),B(-4,0).1.在y轴上是否存在点C,使S△ABC的面积为18?若存在, 2020-07-31 …
二.已知点A(5,0),B(-4,0).1.在y轴上是否存在点C求点C,使S△ABC的面积为18? 2020-07-31 …
已知三角行ABC的面积是根3,角A.B.C所对的边分别为a.b.c且sin的平房=sin的平房A+s 2020-11-02 …
已知直线y=kx+b经过点A(2,4)B(0,-2)(1)求k和b(2)在x轴上是否存在一点C,使△ 2020-11-03 …
班上有四位同学申请A,B,C三所大学的自主招生,若每位同学只能申请其中一所大学,且申请其中任何一所大 2020-12-21 …
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,若AB 2020-12-31 …
三角形ABC中,A,B,C所对的边分别为a,b,c,tanC=sinA+sinB除以cosA+cos 2021-01-23 …