如图，在O中，AB为直径，OC⊥AB，弦CF与OB交于点E，过点F，A分别作O的切线交于点H，且HF与AB的延长线交于点D．（1）求证：DF=DE；（2）若tan∠OCE=12，O的半径为4，求AH的长．

Question

如图，在 O中，AB为直径，OC⊥AB，弦CF与OB交于点E，过点F，A分别作 O的切线交于点H，且HF与AB的延长线交于点D．

（1）求证：DF=DE；
（2）若tan∠OCE=(1)/(2)， O的半径为4，求AH的长．

Answer 1

（1）证明：连结OF，如图，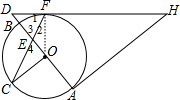
∵DH为切线，
∴OF⊥DH，
∴∠1+∠2=90°，
∵OC⊥AB，
∴∠C+∠4=90°，
∵OF=OC，
∴∠2=∠C，
而∠3=∠4，
∴∠1=∠3，
∴DE=DF；
（2） 在Rt△OEC中，∵tan∠OCE=(OE)/(OC)，
∴OE=(1)/(2)OC=2，
设DF=x，则DE=x，
在Rt△OFD中，x²+4²=（x+2）²，解得x=3，
∴DF=3，DO=5，
∵HF和HA为切线，
∴HF=HA，DA⊥AH，
设AH=t，则HF=t，
在Rt△DAH中，t²+9²=（t+3）²，解得t=12，
即AH的长为12．