早教吧作业答案频道 -->数学-->
如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F(1)探究线段AE、AF的数量关系,并写出解答过程;(2)当点E运动到什么位置时,△AEF的面积最小,最小面
题目详情
如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F
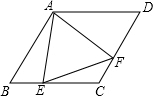
(1)探究线段AE、AF的数量关系,并写出解答过程;
(2)当点E运动到什么位置时,△AEF的面积最小,最小面积是多少?

(1)探究线段AE、AF的数量关系,并写出解答过程;
(2)当点E运动到什么位置时,△AEF的面积最小,最小面积是多少?
▼优质解答
答案和解析
(1)AE=AF,理由如下:
连接AC.如图所示:
∵四边形ABCD是菱形,
∴AB=BC,∵∠B=60°,
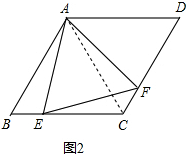 ∴△ABC是等边三角形,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
∴∠B=∠ACF=60°.
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,∠AFC=∠D+∠FAD=60°+∠FAD.
∴∠AEB=∠AFC.
在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS).
∴AE=AF.
(3)由垂线段最短可知:当AE⊥BC时,AE有最小值.
∵AE=AF.∠EAF=60°,
∴△AEF是等边三角形.
∵AE⊥BC,∠B=60°,
∴AE=AB•sin60°=2×
=
,
∴EF=
,此时△AEF的面积=
×
×
×
=
;
当AE⊥BC时,△AEF的面积最小,最小面积是
连接AC.如图所示:
∵四边形ABCD是菱形,
∴AB=BC,∵∠B=60°,
 ∴△ABC是等边三角形,
∴△ABC是等边三角形,∴AB=AC,∠ACB=60°.
∴∠B=∠ACF=60°.
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,∠AFC=∠D+∠FAD=60°+∠FAD.
∴∠AEB=∠AFC.
在△ABE和△ACF中,
|
∴△ABE≌△ACF(AAS).
∴AE=AF.
(3)由垂线段最短可知:当AE⊥BC时,AE有最小值.
∵AE=AF.∠EAF=60°,
∴△AEF是等边三角形.
∵AE⊥BC,∠B=60°,
∴AE=AB•sin60°=2×
| ||
| 2 |
| 3 |
∴EF=
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
3
| ||
| 4 |
当AE⊥BC时,△AEF的面积最小,最小面积是
3
|
看了 如图,在菱形ABCD中,∠B...的网友还看了以下:
已知F(x)=1+2+3+………………+n(n属于自然数),则lim{f(n^2)}/{f(n)}^ 2020-03-31 …
1、已知函数f(x)=ax2+2ax+4(a>0),若x1<x2,x1+x2=0,则()a.f(x 2020-04-25 …
已知f(x)是定义在R上的奇函数,且当x<0时,f(x)=2^x+1.(1)求函数f(x)的解析式 2020-05-15 …
(1)logaN^n=nlogaN求推导公式(2)已知a=lgx,则a+x等于?(3)若2.5^x 2020-05-16 …
1、已知函数f(x)的定义域是[0,1]。求f(x-2),f(x-1),f(2x-2)的定义域。变 2020-05-17 …
已知f(x)=log31/4-x,x属于I-5,35/9I(1)求f(x)关于点(2,1)对称的函 2020-05-23 …
已知函数f(x)的定义域为R,对任意实数m,n,满足f(1/2)=2,且f(m+n)=f(m)+f 2020-06-03 …
已知函数f(x)是(负无穷,正无穷)上得奇函数,且f(x)的图像关于x=1对称当x属于[0,1]时 2020-06-09 …
已知函数y=f(x)的定义域为[-2,4],则f(x+1)的定义域为已知y=f(x+2)的定义域为 2020-06-25 …
涵数F(X)有关定义域1.设涵数F(X)=2X-1则F(X+1)F(F(X))2.涵数F(X)的定 2020-06-29 …
 扫描下载二维码
扫描下载二维码