早教吧作业答案频道 -->数学-->
如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60c,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿C方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB
题目详情
如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60c,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿C方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB方向移动.设移动时间为t(s),以点P为圆心,3t(cm)长为半径的⊙P与AB相交于点M,N,当点F与点A重合时,△DEF与点P同时停止移动,在移动过程中,
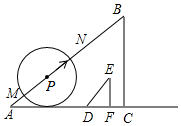
(1)连接ME,当ME∥AC时,t=___s;
(2)连接NF,当NF平分DE时,求t的值;
(3)是否存在⊙P与Rt△DEF的两条直角边所在的直线同时相切的时刻?若存在,求出t的值;若不存在,说明理由.

(1)连接ME,当ME∥AC时,t=___s;
(2)连接NF,当NF平分DE时,求t的值;
(3)是否存在⊙P与Rt△DEF的两条直角边所在的直线同时相切的时刻?若存在,求出t的值;若不存在,说明理由.
▼优质解答
答案和解析
(1)如图1所示:作MH⊥AC,垂足为H,作OG⊥AC,垂足为G.
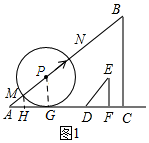
∵在Rt△ABC中,AC=60,BC=45,
∴AB=75cm.
∴sin∠A=
.
∴PM=PG=
PA=3t.
∴AM=5t-3t=2t.
∴HM=
AM=
t.
当ME∥AC时,MH=EF,即
t=8,解得t=
.
故答案为:
.
(2)如图2所示:连结NF交DE与点G,则G为DE的中点.
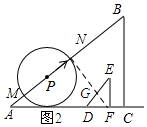
∵AC=60cm,BC=45cm,DF=6cm,EF=8cm,
∴
=
.
又∵∠ACB=∠DFE=90°,
∴△EDF∽△ABC.
∴∠A=∠E.
∵E是DE的中点,
∴GF=DG=
ED.
∴∠DFD=∠GDF.
∵∠GDF+∠E=90°,
∴∠GFD+∠E=90°.
∴∠A+∠GFD=90°.
∴∠ANF=90°.
∴AF=
AN=10t.
又∵FC=4t,
∴10t+4t=60,解得t=
.
(3)如图3所示:过点P作PH⊥AC,垂足为H,当⊙P与EF相切时,且点为G,连结PG.
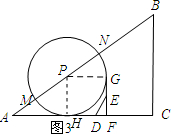
∵EF是⊙P的切线,
∴∠PGF=90°.
∵∠PGF=∠GFH=∠PHF=90°,
∴四边形PGFH为矩形.
∴PG=HF.
∵⊙P的半径为3t,sin∠A=
,AP=5t,
∴PH=3t.
∴⊙P与AC相切.
∵EF为⊙P的切线,
∴PG⊥EF.
∴HF=PG=3t.
∵AH=
AP=4t,FC=4t,
∴4t+3t+4t=60,解得t=
.
如图4所示:连接GP,过点P作PH⊥AC,垂足为H.
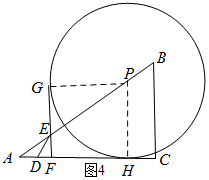
由题意得可知:AH=4t,CF=4t.
∵EF是⊙P的切线,
∴∠PGF=90°.
∵∠PGF=∠GFH=∠PHF=90°,
∴四边形PGFH为矩形.
∴PG=HF.
∵GP=FH,
∴FH=3t.
∴4t+4t-3t=60,解得:t=12.
综上所述,当t的值为
或12时,⊙P与Rt△DEF的两条直角边所在的直线同时相切.

∵在Rt△ABC中,AC=60,BC=45,
∴AB=75cm.
∴sin∠A=
| 3 |
| 5 |
∴PM=PG=
| 3 |
| 5 |
∴AM=5t-3t=2t.
∴HM=
| 3 |
| 5 |
| 6 |
| 5 |
当ME∥AC时,MH=EF,即
| 6 |
| 5 |
| 20 |
| 3 |
故答案为:
| 20 |
| 3 |
(2)如图2所示:连结NF交DE与点G,则G为DE的中点.

∵AC=60cm,BC=45cm,DF=6cm,EF=8cm,
∴
| BC |
| DF |
| AC |
| EF |
又∵∠ACB=∠DFE=90°,
∴△EDF∽△ABC.
∴∠A=∠E.
∵E是DE的中点,
∴GF=DG=
| 1 |
| 2 |
∴∠DFD=∠GDF.
∵∠GDF+∠E=90°,
∴∠GFD+∠E=90°.
∴∠A+∠GFD=90°.
∴∠ANF=90°.
∴AF=
| 5 |
| 4 |
又∵FC=4t,
∴10t+4t=60,解得t=
| 30 |
| 7 |
(3)如图3所示:过点P作PH⊥AC,垂足为H,当⊙P与EF相切时,且点为G,连结PG.

∵EF是⊙P的切线,
∴∠PGF=90°.
∵∠PGF=∠GFH=∠PHF=90°,
∴四边形PGFH为矩形.
∴PG=HF.
∵⊙P的半径为3t,sin∠A=
| 3 |
| 5 |
∴PH=3t.
∴⊙P与AC相切.
∵EF为⊙P的切线,
∴PG⊥EF.
∴HF=PG=3t.
∵AH=
| 4 |
| 5 |
∴4t+3t+4t=60,解得t=
| 60 |
| 11 |
如图4所示:连接GP,过点P作PH⊥AC,垂足为H.

由题意得可知:AH=4t,CF=4t.
∵EF是⊙P的切线,
∴∠PGF=90°.
∵∠PGF=∠GFH=∠PHF=90°,
∴四边形PGFH为矩形.
∴PG=HF.
∵GP=FH,
∴FH=3t.
∴4t+4t-3t=60,解得:t=12.
综上所述,当t的值为
| 60 |
| 11 |
看了 如图,已知Rt△ABC的直角...的网友还看了以下:
高数题解设f(x)以T(>0)为周期,求函数的周期.f(x+2) 2020-04-26 …
设函数f(x)连续且恒大于零,F(t)=∫∫∫Ω(t)f(x2+y2+z2)dv∫∫D(t)f(x 2020-06-12 …
F(X)在区间I上可导若F(X)以T为周期,求证F‘(X)以T为周期 2020-06-18 …
关于周期问题的高数选择和一道比大小(1)f(x)是以T为周期的可微函数,下列也是以T为周期的函数是 2020-07-07 …
200分真心讨教高数定积分知识假定函数f(X)以T为周期即对于任意的实数x有f(x+t)=f(x) 2020-07-09 …
这道积分怎么证明设函数f(x)以T为周期,证明a+TT∫f(x)dx=∫f(x)dx(a为常数)a 2020-07-09 …
readyfordry服装英语简写是R.F.D.,我同事说是readyfordry,但是我有点不理 2020-07-23 …
已知函数f(x)的定义域为D,若存在非零常数t,使得对于任意x∈M(M⊆D),有x+t∈D,且f( 2020-08-01 …
关于周期函数积分的问题,有一个定理理解不了,假定周期函数f(x)以T为周期,则f(x)的全体原函数 2020-08-01 …
周期函数的积分问题f(x)以T为周期,则积分0→Tf(x)dx=0可为什么|sinx|的周期为pi 2020-08-01 …