设函数f(x)＝x2＋x，当x∈[n，n＋1](n∈N*)时，f(x)的所有整数值的个数为g(n)．(1)求g(n)的表达式；(2)设bn＝，Tn＝b1＋b2＋…＋bn若Tn＜l(l∈Z)，求l的最小值(3)设a
设函数f(x)＝x 2 ＋x，当x∈[n，n＋1](n∈N * )时，f(x)的所有整数值的个数为g(n)．
(1)求g(n)的表达式；
(2)设b n ＝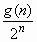
，T n ＝b 1 ＋b 2 ＋…＋b n 若T n ＜ l ( l ∈Z)，求 l 的最小值
(3)设a n ＝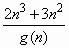
(n∈N * )，S n ＝a 1 －a 2 ＋a 3 －a 4 ＋…＋(－1) n－1 a n ，求S n ；
解析：
(1)当时，函数的值随x的增大而增大， ∴的值域为，∴． (2)由① ①×得② ①－②得 ＝． ∴． 则由，可得l的最小值是7． (3)． ①n为偶数时， ＝－[3＋7＋…＋(2n－1)]＝－．
数学达人请进（概率和数理统计）设随机变量§和n相互独立,且均服从两点分布B(1,p),求(§,n) 2020-04-27 …
(1+x)+(1+x)^2+(1+x)^3+.+(1+x)^n=a0+a1*x+a2*x^2+.a 2020-05-20 …
如图，在平面直角坐标系xOy中，将二次函数y=x2-1的图象M沿x轴翻折，把所得到的图象向右平移2 2020-06-14 …
已知n属正整数,（2x-1/x)^n=anx^n+an-1xn-1+...+a1-nx^1-n+a 2020-07-31 …
请问下列数学题除了列举法外还有什么好办法解题：设N是正整数,且使得[1÷(1+n)+1÷(4+n) 2020-08-01 …
已知n∈N*，在（x+2）n的展开式中，第二项系数是第三项系数的15．（1）求n的值；（2）求展开 2020-08-03 …
已知n（n∈N*）满足3Cn−5n−1＝5P2n−2，整数a是413+C113412+C21341 2020-08-03 …
已知f(x)＝(x1k+x)n，且正整数n满足C2n＝C6n，A＝{0，1，2，…n}．（1）求n； 2020-10-31 …
1、在等比数列{an}中,已知a3+a6=36,a4+a7=18,an=1/2,求n的值2、已知等比 2020-11-27 …
x1=2,xn+1=2+1/n,n=1,2,……,求n趋于无穷时,xn的值答案我知道怎么求,不过过程 2020-12-31 …