早教吧作业答案频道 -->数学-->
如图,已知∠MBN=60°,在BM,BN上分别截取BA=BC,P是∠MBN内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;(2)若PA
题目详情
如图,已知∠MBN=60°,在BM,BN上分别截取BA=BC,P是∠MBN内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
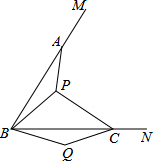
(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2)若PA:PB:PC=3:4:5,连接PQ,求证:∠PQC=90°.

(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2)若PA:PB:PC=3:4:5,连接PQ,求证:∠PQC=90°.
▼优质解答
答案和解析
(1) AP=CQ;理由如下: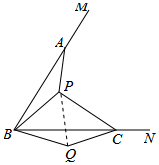
连接PQ,如图所示:
∵∠PBQ=60°,且BQ=BP,
∴△BPQ为等边三角形,
∵∠ABP+∠CBP=60°,∠CBQ+∠CBP=60°,
∴∠CBQ=∠ABP,
在△ABP和△CBQ中,
,
∴△ABP≌△CBQ(SAS),
∴AP=CQ,
(2)证明:设PA=3a,PB=4a,PC=5a,
在△PBQ中,∵PB=BQ=4a,且∠PBQ=60°,
∴△PBQ为等边三角形,
∴PQ=4a,
在△PQC中,∵PQ2+QC2=16a2+9a2=25a2=PC2,
∴△PQC为直角三角形,即∠PQC=90°.

连接PQ,如图所示:
∵∠PBQ=60°,且BQ=BP,
∴△BPQ为等边三角形,
∵∠ABP+∠CBP=60°,∠CBQ+∠CBP=60°,
∴∠CBQ=∠ABP,
在△ABP和△CBQ中,
|
∴△ABP≌△CBQ(SAS),
∴AP=CQ,
(2)证明:设PA=3a,PB=4a,PC=5a,
在△PBQ中,∵PB=BQ=4a,且∠PBQ=60°,
∴△PBQ为等边三角形,
∴PQ=4a,
在△PQC中,∵PQ2+QC2=16a2+9a2=25a2=PC2,
∴△PQC为直角三角形,即∠PQC=90°.
看了 如图,已知∠MBN=60°,...的网友还看了以下:
设点A(1,0)B(2,1)如果直线ax+by=1与线段AB有一个公共点,那么a^2+b^2的最值 2020-04-25 …
如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC 2020-05-16 …
已知ABC中,点A,B的坐标分别为(-√2,0)(√2,0)点C在X轴上方若点C坐标(√2,1), 2020-06-21 …
已知菱形ABCD的对角线交于点O,AC=6,BD=8,以A为圆心,r为半径画⊙A,对于B,C,D, 2020-07-26 …
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中 2020-12-21 …
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1,以A为中心顺时针旋转点M,以B为中 2020-12-21 …
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1,以A为中心顺时针旋转点M,以B为中 2020-12-21 …
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中 2020-12-21 …
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中 2020-12-21 …
(2014•南开区二模)如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心 2020-12-21 …