早教吧作业答案频道 -->数学-->
已知a为实数,函数f(x)=x2-|x2-ax-2|在区间(-∞,-1)和(2,+∞)上单调递增,则a的取值范围为()A.[1,8]B.[3,8]C.[1,3]D.[-1,8]
题目详情
已知a为实数,函数f(x)=x2-|x2-ax-2|在区间(-∞,-1)和(2,+∞)上单调递增,则a的取值范围为( )
A. [1,8]
B. [3,8]
C. [1,3]
D. [-1,8]
▼优质解答
答案和解析
令函数g(x)=x2-ax-2,由于g(x)的判别式△=a2+8>0,故函数g(x)一定有两个零点,
设为x1 和x2,且 x12.
∵函数f(x)=x2-|x2-ax-2|=
,
故当x∈(-∞,x1)、(x2,+∞)时,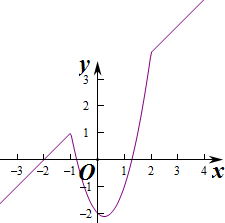
函数f(x)的图象是位于同一条直线上的两条射线,
当x∈(x1,x2 )时,函数f(x)的图象是抛物线y=2x2-ax-2下凹的一部分,且各段连在一起.
由于f(x)在区间(-∞,-1)和(2,+∞)上单调递增,
∴a>0且函数g(x)较小的零点x1=
≥-1,
即a+2≥
,
平方得a2+4a+4≥a2+8,得a≥1,
同时由y=2x2-ax-2的对称轴为x=
,
若且-1≤
≤2,可得-4≤a≤8.
综上可得,1≤a≤8,
故实a的取值范围为[1,8],
故选:A.
设为x1 和x2,且 x1
∵函数f(x)=x2-|x2-ax-2|=
|
故当x∈(-∞,x1)、(x2,+∞)时,
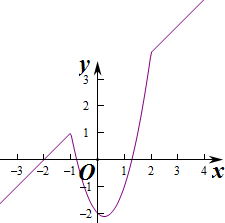
函数f(x)的图象是位于同一条直线上的两条射线,
当x∈(x1,x2 )时,函数f(x)的图象是抛物线y=2x2-ax-2下凹的一部分,且各段连在一起.
由于f(x)在区间(-∞,-1)和(2,+∞)上单调递增,
∴a>0且函数g(x)较小的零点x1=
a-
| ||
| 2 |
即a+2≥
| a2+8 |
平方得a2+4a+4≥a2+8,得a≥1,
同时由y=2x2-ax-2的对称轴为x=
| a |
| 4 |
若且-1≤
| a |
| 4 |
综上可得,1≤a≤8,
故实a的取值范围为[1,8],
故选:A.
看了 已知a为实数,函数f(x)=...的网友还看了以下:
有几条数学竞赛题,要挑战自己数学能力的就进来吧!5.在自变量x的取值范围59≤x≤60内,二次函数 2020-04-26 …
已知x1和x2是方程x2+3x+1=0的两个实数根,则x13+8 x2+20= 2020-05-16 …
已知数据x1,x2……xn的平均数是3,则一组新数据x1+8,x2+8……x3+8的平均数是? 2020-05-17 …
一道有关二次函数的初三数学题已知关于x的二次函数x2+2(m+1)x+m2-1,求证:(1)不论m 2020-05-17 …
已知y=x2+bx+c的图象向右平移2个单位长度,再向下平移3个单位长度,得到的图象对应的函数表达 2020-06-14 …
已知二次函y=x2+px+q图象的顶点M为直线y=12x+12与y=-x+m-1的交点.(1)用含 2020-07-14 …
设A∈R5*4,R(A)=2,已知x1,x2,x3为Ax=b的三个解,且x1+x2=(4,6,-8 2020-07-31 …
已知x1、x2、x3、x4、x5是非负实数已知x1,x2,x3,x4,x5是非负实数,且x1+x2+ 2020-10-31 …
我们知道x2+6x+9可以因式分解为(x+3)2,其实x2+6x+8及2x2+6x-6也可以通过配方 2020-11-03 …
因式分解与整式乘法是方向相反的变形.∵(x+4)(x+2)=x2+6x+8∴x2+6x+8=(x+4 2020-11-03 …