如图，E、F、G、H分别是空间四边形ABCD各边上的点，且有AE∶EB=AH∶HD=mCF∶FB=CG∶GD=n.(1)证明E、F、G、H四点共面.(2)m、n满足什么条件时，EFGH是平行四边形?(3)在(2)的条件下，若AC

Question

如图，E、F、G、H分别是空间四边形ABCD各边上的点，且有AE∶EB=AH∶HD=m CF∶FB=CG∶GD=n.

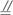
(1)证明E、F、G、H四点共面.

(2)m、n满足什么条件时，EFGH是平行四边形?

(3)在(2)的条件下，若AC⊥BD，试证明EG=FH.

Answer 1

(1)证明:∵AE∶EB=AH∶HD，∴EH∥BD.∵CF∶FB=CG∶GD，∴FG∥BD.∴EH∥FG.∴E、F、G、H四点共面.(2)解:当且仅当EHFG时，四边形EFGH为平行四边形.∵ ∴EH=BD.同理 FG=BD.由EH=FG得m=n.故当m=n时，四边形EFGH为平行四边形.(3)证明:当m=n时，AE∶EB=CF∶FB ∴EF∥AC.又∵AC⊥BD，∴∠FEH是AC与BD所成的角.∴∠FEH=90°.从而EFGH为矩形，∴EG=FH.点评:空间四边形是立体几何的一个基本图形，它各边中点的连线构成平行四边形；当两对角线相等时该平行四边形为菱形；当两对角线互相垂直时，该平行四边形为矩形；当两对角线相等且互相垂直时 该平行四边形为正方形.