早教吧作业答案频道 -->数学-->
已知直线y=-43x+4与x轴和y轴分别交与A、B两点,另一直线过点A和点C(7,3).(1)求直线AC对应的函数关系式;(2)求证:AB⊥AC;(3)若点P是直线AC上的一个动点,点Q是x轴上的一个动点,
题目详情
已知直线y=-
x+4与x轴和y轴分别交与A、B两点,另一直线过点A和点C(7,3).
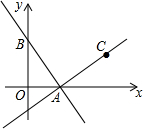
(1)求直线AC对应的函数关系式;
(2)求证:AB⊥AC;
(3)若点P是直线AC上的一个动点,点Q是x轴上的一个动点,且以P、Q、A为顶点的三角形与△AOB全等,求点Q的坐标.
| 4 |
| 3 |

(1)求直线AC对应的函数关系式;
(2)求证:AB⊥AC;
(3)若点P是直线AC上的一个动点,点Q是x轴上的一个动点,且以P、Q、A为顶点的三角形与△AOB全等,求点Q的坐标.
▼优质解答
答案和解析
(1)在y=-
x+4中,
令y=0,则0=-
x+4,
∴x=3,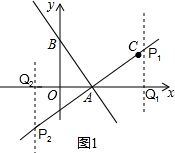
∴A(3,0),
设直线AC对应的函数关系式为y=kx+b,
∴
,
∴
,
∴直线AC对应的函数关系式为y=
x-
,
(2)在直线ABy=-
x+4中,∵k1=-
,
在直线ACy=
x-
中,k2=
,
∴k1•k2=-1,
∴AB⊥AC;
(3)在y=-
x+4中,
令x=0,则y=4,
∴OA=3,OB=4,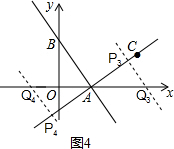 由勾股定理得AB=5,
由勾股定理得AB=5,
①当∠AQP=90°时,如图1,∵△AOB≌△AQP,
∴AQ=OB=4,
∴Q1(7,0),Q2(-1,0),
②当∠APQ=90°时,如图2,∵△AOB≌△AQP,
∴AQ=AB=5,
∴Q3(8,0),Q4(-2,0).
③当∠PAQ=90°时,这种情况不存在,
综上所述:点Q的坐标为:(7,0)(8,0)(-1,0)(-2,0).
| 4 |
| 3 |
令y=0,则0=-
| 4 |
| 3 |
∴x=3,

∴A(3,0),
设直线AC对应的函数关系式为y=kx+b,
∴
|
∴
|
∴直线AC对应的函数关系式为y=
| 3 |
| 4 |
| 9 |
| 4 |
(2)在直线ABy=-
| 4 |
| 3 |
| 4 |
| 3 |
在直线ACy=
| 3 |
| 4 |
| 9 |
| 4 |
| 3 |
| 4 |
∴k1•k2=-1,
∴AB⊥AC;
(3)在y=-
| 4 |
| 3 |
令x=0,则y=4,
∴OA=3,OB=4,
 由勾股定理得AB=5,
由勾股定理得AB=5,①当∠AQP=90°时,如图1,∵△AOB≌△AQP,
∴AQ=OB=4,
∴Q1(7,0),Q2(-1,0),
②当∠APQ=90°时,如图2,∵△AOB≌△AQP,
∴AQ=AB=5,
∴Q3(8,0),Q4(-2,0).
③当∠PAQ=90°时,这种情况不存在,
综上所述:点Q的坐标为:(7,0)(8,0)(-1,0)(-2,0).
看了已知直线y=-43x+4与x轴...的网友还看了以下:
已知等比数列{an}中,a1=1/3,公比q=1/3.求Sn为{an}的前n项和,证明:Sn=1- 2020-04-06 …
如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B 2020-05-13 …
如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B 2020-05-13 …
圆O和圆Q都经过点A和B,PR切圆Q于p,交圆O于R,M,交AB的延长线于N.求证:PN^2=NM 2020-05-13 …
如图甲所示,水平传送带顺时针方向匀速运动。从传送带左端P先后由静止轻轻放上三个物体A、B、C,物体 2020-06-16 …
已知点A(-1,0),B(1,-1)和抛物线C:y2=4x,O为坐标原点,过点A的动直线l交抛物线 2020-07-24 …
数学题急已知点A(-1,0),B(-1,1)和抛物线C:y^2=4x,O为坐标原点,过点A的动直线 2020-07-24 …
(1/2)等比(an)数列的前n项和与积分别为S和T,数列(an分之一)的前n项和为Q,求证T的平 2020-07-28 …
已知抛物线C:x2=2py(p>0),其焦点F到准线的距离为.(1)试求抛物线C的方程;(2)设抛 2020-07-31 …
已知抛物线cy22px设抛物线上一点p的横坐标为t过p的直线交c与另一点已知抛物线C:y=x^2上一 2020-11-27 …