早教吧作业答案频道 -->数学-->
如图,在Rt△AOB中,∠ABO=30°,BO=4,分别以OA、OB边所在的直线建立平面直角坐标系,D点为x轴正半轴上的一点,以OD为一边在第一象限内作等边△ODE.(Ⅰ)如图①当E点恰好落在线段AB上时,
题目详情
如图,在Rt△AOB中,∠ABO=30°,BO=4,分别以OA、OB边所在的直线建立平面直角坐标系,D点为x轴正半轴上的一点,以OD为一边在第一象限内作等边△ODE.
(Ⅰ)如图①当E点恰好落在线段AB上时,求E点坐标;
(Ⅱ)若点D从原点出发沿x轴正方向移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,当E点到达△AOB的外面,且点D在点B左侧时,写出y与x的函数关系式,并写出自变量x的取值范围;
(Ⅲ)在(Ⅰ)问的条件下,将△ODE在线段OB上向右平移如图②,图中是否存在一条与线段OO′始终相等的线段?如果存在,请直接指出这条线段;如果不存在,请说明理由.
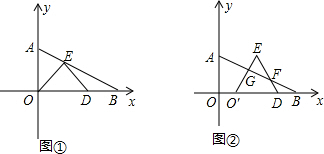
(Ⅰ)如图①当E点恰好落在线段AB上时,求E点坐标;
(Ⅱ)若点D从原点出发沿x轴正方向移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,当E点到达△AOB的外面,且点D在点B左侧时,写出y与x的函数关系式,并写出自变量x的取值范围;
(Ⅲ)在(Ⅰ)问的条件下,将△ODE在线段OB上向右平移如图②,图中是否存在一条与线段OO′始终相等的线段?如果存在,请直接指出这条线段;如果不存在,请说明理由.

▼优质解答
答案和解析
(1)作EH⊥OB于点H,
∵△OED是等边三角形,
∴∠EOD=60°.
又∵∠ABO=30°,
∴∠OEB=90°.
∵BO=4,
∴OE=
OB=2.
∵△OEH是直角三角形,且∠OEH=30°
∴OH=1,EH=
,
∴E(1,
).
(2)当2<x<4,符合题意,
如图,
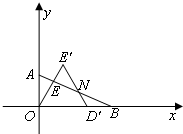
所求重叠部分四边形OD′NE的面积为:
S△OD′E-S△E′EN=
x2-
E′E×EN
=
x2-
×
(x-2)
=-
x2+2
x-2
(3)存在线段EF=OO'.
∵∠ABO=30°,∠EDO=60°
∴∠ABO=∠DFB=30°,
∴DF=DB.
∴OO′=4-2-DB=2-DB=2-DF=ED-FD=EF
∵△OED是等边三角形,
∴∠EOD=60°.
又∵∠ABO=30°,
∴∠OEB=90°.
∵BO=4,
∴OE=
| 1 |
| 2 |
∵△OEH是直角三角形,且∠OEH=30°
∴OH=1,EH=
| 3 |
∴E(1,
| 3 |
(2)当2<x<4,符合题意,
如图,

所求重叠部分四边形OD′NE的面积为:
S△OD′E-S△E′EN=
| ||
| 4 |
| 1 |
| 2 |
=
| ||
| 4 |
| x-2 |
| 2 |
| 3 |
=-
| ||
| 4 |
| 3 |
| 3 |
(3)存在线段EF=OO'.
∵∠ABO=30°,∠EDO=60°
∴∠ABO=∠DFB=30°,
∴DF=DB.
∴OO′=4-2-DB=2-DB=2-DF=ED-FD=EF
看了 如图,在Rt△AOB中,∠A...的网友还看了以下:
从1、2、3、4、5五个数字中等可能地,有放回地抽取3个数字,求下列各事件的概率.(1)A={3个 2020-05-13 …
EXCEL公式有什么区别,第一个括号前2个条件,第二个括号3个条件?=SUMPRODUCT(($B 2020-05-15 …
一次函数y=1/3+1的图像与x轴,y轴分别交与A,B,点C的坐标为(2,0)(1)求直线BC的函 2020-06-14 …
已知两圆内切,它们的半径分别为3和6,则这两圆的圆心距d的取值满足()A.d>9B.d=9C.3< 2020-06-27 …
16、已知两圆内切,它们的半径分别为3和6,则这两圆的圆心距d的取值满足()A、d>9B、d=9C 2020-06-27 …
已知两圆内切,它们的半径分别为3和6,则这两圆的圆心距d的取值满足()A.d>9B.d=9C.3< 2020-06-27 …
英语翻译1.我决不能让那个坏人做那种坏事而不受惩罚2.根据我的研究,我们俩家都不能提供均衡的膳食3 2020-07-01 …
判别向量组的线性相关性a1=|1,a,a^2,a^3|,a2=|1,b,b^2,b^3|,a3=| 2020-07-09 …
如图,如图矩形abcd中,把∠b,∠d分别翻折,使点b,d恰好落在对角线ac上的点e,f处,折,使 2020-07-22 …
数学选择题:下列计算运算律恰当的有()(1)28+(-18)+6+(-21)=[(-18)+(-2 2020-07-31 …