早教吧作业答案频道 -->数学-->
如图,将抛物线y=x2向右平移a个单位长度,顶点为A,与y轴交于点B,且△AOB为等腰直角三角形.(1)求a的值;(2)在图中的抛物线上是否存在点C,使△ABC为等腰直角三角形?若存在,直接
题目详情
如图,将抛物线y=x2向右平移a个单位长度,顶点为A,与y轴交于点B,且△AOB为等腰直角三角形.
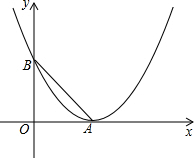
(1)求a的值;
(2)在图中的抛物线上是否存在点C,使△ABC为等腰直角三角形?若存在,直接写出点C的坐标,并求S△ABC;若不存在,请说明理由.

(1)求a的值;
(2)在图中的抛物线上是否存在点C,使△ABC为等腰直角三角形?若存在,直接写出点C的坐标,并求S△ABC;若不存在,请说明理由.
▼优质解答
答案和解析
(1)平移后的抛物线的解析式为y=(x-a)2=x2-2ax+a2,
令y=x2-2ax+a2中x=0,则y=a2,
∴B(0,a2).
∵△AOB为等腰直角三角形,
∴a=a2,解得:a=1或a=0(舍去).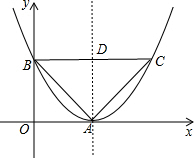
故a的值为1.
(2)作点B关于抛物线对称轴对称的点C,连接BC,交抛物线的对称轴于点D,如图所示.
∵△AOB为等腰直角三角形,
∴△ABD为等腰直角三角形,
∴∠BAD=45°.
∵AD为抛物线的对称轴,
∴AB=AC,∠CAD=∠BAD=45°,
∴△ABC为等腰直角三角形.
∵点B(0,1),抛物线对称轴为x=1,
∴点C的坐标为(2,1).
S△ABC=
AB•AC=
×
×
=1.
故在图中的抛物线上存在点C,使△ABC为等腰直角三角形,点C的坐标为(2,1)且S△ABC=1.
令y=x2-2ax+a2中x=0,则y=a2,
∴B(0,a2).
∵△AOB为等腰直角三角形,
∴a=a2,解得:a=1或a=0(舍去).

故a的值为1.
(2)作点B关于抛物线对称轴对称的点C,连接BC,交抛物线的对称轴于点D,如图所示.
∵△AOB为等腰直角三角形,
∴△ABD为等腰直角三角形,
∴∠BAD=45°.
∵AD为抛物线的对称轴,
∴AB=AC,∠CAD=∠BAD=45°,
∴△ABC为等腰直角三角形.
∵点B(0,1),抛物线对称轴为x=1,
∴点C的坐标为(2,1).
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故在图中的抛物线上存在点C,使△ABC为等腰直角三角形,点C的坐标为(2,1)且S△ABC=1.
看了如图,将抛物线y=x2向右平移...的网友还看了以下:
求复合下列条件的抛物线y=ax^2的表达式.1.抛物线y=ax^2于y=3分之2x^2的图像开口大小 2020-03-30 …
开口向上的抛物线y=a(x+k)2的展开式为y=ax2+2akx+ak2,若抛物线于y轴交点的纵坐 2020-06-12 …
若抛物线Y=x的平方-2X+c于Y轴的交点坐标为(0,-3),则下列说法不正确的是()A.抛物线的 2020-06-12 …
一道二次函数小题已知抛物线y=-x^2+2x.过抛物线上一点P(x,y)向直线y=5/4做垂线,垂 2020-07-14 …
已知抛物线y=-x^2+2x.过抛物线上一点P(x,y)向直线y=5/4做垂线,垂足为M.请问:对 2020-07-14 …
如图,抛物线y=x2-2x-3交x轴于A(-1,0)、B(3,0),交y轴于C(0,-3),M是抛 2020-07-20 …
如图,过y轴上一点A(0,1)作AC平行于x轴,交抛物线如图,过y轴上一点A(0,1)作AC平行X 2020-07-29 …
1.已知抛物线y=ax方经过a(2,1)1)写出抛物线上a关于y轴的对称点b的坐标2)求oab的面 2020-08-02 …
:一抛物线的轴平衡于X轴开口向左且通过原定和店(2,1)求当它于Y轴所围的面积最小时的方程一抛物线的 2020-11-04 …
在同一坐标系中,作y=2x2,y=-2x2,y=12x2的图象,他们共同的特点是()A.都关于y轴对 2020-11-04 …