早教吧作业答案频道 -->数学-->
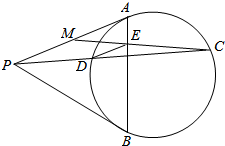
如图,过圆外一点P分别作O的两条切线PA,PB和一条割线PDC,记PA的中点为M,连接CM与AB交于点E.求证:DE∥PA.
题目详情
如图,过圆外一点P分别作 O的两条切线PA,PB和一条割线PDC,记PA的中点为M,连接CM与AB交于点E.求证:DE∥PA.

▼优质解答
答案和解析
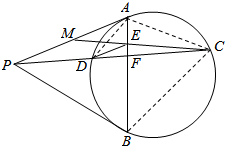 证明:设AB,CD的交点为F,连接BC,AD,AC
证明:设AB,CD的交点为F,连接BC,AD,AC
则由切割线定理知△PBD∽△PCB,△PAD∽△PCA
即有
=
=
,
=
=
,
又PA=PB
∴
=
•
=
•
=
•
=
=
而PB2=PD•PC,∴
=
∴
=
又C,E,M为△APF的割线,M为AP中点
∴由梅涅劳斯定理
•
•
=1
可得
=
=
,∴DE∥AP
 证明:设AB,CD的交点为F,连接BC,AD,AC
证明:设AB,CD的交点为F,连接BC,AD,AC则由切割线定理知△PBD∽△PCB,△PAD∽△PCA
即有
| PB |
| PC |
| PD |
| DB |
| BD |
| BC |
| PA |
| PC |
| PD |
| PA |
| AD |
| AC |
又PA=PB
∴
| PB2 |
| PC2 |
| BD |
| BC |
| AD |
| AC |
| BD |
| BC |
| AD |
| BC |
| DF |
| AF |
| DF |
| BF |
| DF2 |
| DF•CF |
| DF |
| CF |
而PB2=PD•PC,∴
| PD |
| PC |
| DF |
| CF |
∴
| DF |
| PD |
| CF |
| PC |
又C,E,M为△APF的割线,M为AP中点
∴由梅涅劳斯定理
| AM |
| MP |
| PC |
| CF |
| FE |
| EA |
可得
| FE |
| EA |
| CF |
| PC |
| DF |
| PD |
看了如图,过圆外一点P分别作O的两...的网友还看了以下:
已知M是抛物线C:x^2=4y上的动点,过M作y轴的垂线MN,垂足为N,记线段MN的中点为E.(1 2020-04-13 …
已知M是抛物线C:x^2=4y上的动点,过M作y轴的垂线MN,垂足为N,记线段MN的中点为E.(1 2020-04-13 …
二次函数E(3,0)为圆心以5为半径的园E与X轴交于C点,抛物线Y=aX²+bX+c经过A,B,C 2020-05-13 …
(2014•龙东地区)已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m 2020-06-15 …
重组字母为单词e,e,r,w,he,e,r,t,he,e,se,a,sw,m,s,ir,t,p,i 2020-07-09 …
如图,已知点P(1,3)在函数y=k/x(x>0)的图像上,矩形ABCD的边BC在x轴上,E是对角 2020-08-01 …
如图所示,已知点(1,3)在函数y=k/x(x>0)的图象上,矩形ABCD的边BC在X轴上,E是对 2020-08-01 …
惫设f(x)=-m(m+e)x2,g(x)=x2+(m-1)x-m,其中e均自然对数的底数,若∃x 2020-08-02 …
数学椭圆的题参数方程已知M(2,1)和椭圆C:x^2+4y^2=16,过M作C的一条弦AB,使M为 2020-08-02 …
如图,点E、M分别是正方形ABCD边的AB、CD上的动点,连结DE,过M作MF⊥DE于H,交AD于点 2020-11-01 …