早教吧作业答案频道 -->数学-->
(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;(2)O是正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.①在图
题目详情
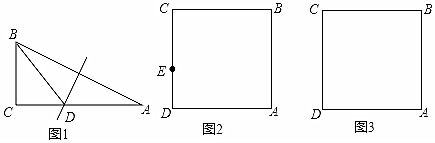
(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;
(2)O是正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中作出△EDF,有适当的文字说明,并求出∠EOF的度数;
②若
=
,求
的值.
(2)O是正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中作出△EDF,有适当的文字说明,并求出∠EOF的度数;
②若
| OF |
| OE |
2
| ||
| 3 |
| AF |
| CE |

▼优质解答
答案和解析
(1) ∵AB的垂直平分线交AC于点D,
∵AB的垂直平分线交AC于点D,
∴BD=AD,
∴△BCD的周长=BC+CD+BD=BC+AC=1+2=3,
故答案为:3;
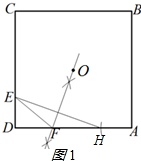
(2)①如图1所示:△EDF即为所求;
如图2所示:AH=DE,
连接OA、OD、OH,
∵点O为正方形ABCD的中心,
∴OA=OD,∠AOD=90°,∠1=∠2=45°,
在△ODE和△OAH中,
,
∴△ODE≌△OAH(SAS),
∴∠DOE=∠AOH,OE=OH,
∴∠EOH=90°,
∵△EDF的周长等于AD的长,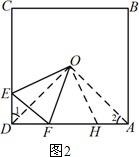
∴EF=HF,
在△EOF和△HOF中,
,
∴△EOF≌△HOF(SSS),
∴∠EOF=∠HOF=45°;
②连接OC,
∵∠ECO=∠EOF=∠OAF=45°,∠EOC=∠AFO,
∴△COE∽△AFO,
∴
=
=
,
∴
•
=
•
∴
=(
)2=(
)2=
.
 ∵AB的垂直平分线交AC于点D,
∵AB的垂直平分线交AC于点D,∴BD=AD,
∴△BCD的周长=BC+CD+BD=BC+AC=1+2=3,
故答案为:3;
(2)①如图1所示:△EDF即为所求;
如图2所示:AH=DE,
连接OA、OD、OH,
∵点O为正方形ABCD的中心,
∴OA=OD,∠AOD=90°,∠1=∠2=45°,
在△ODE和△OAH中,
|
∴△ODE≌△OAH(SAS),
∴∠DOE=∠AOH,OE=OH,
∴∠EOH=90°,
∵△EDF的周长等于AD的长,

∴EF=HF,
在△EOF和△HOF中,
|
∴△EOF≌△HOF(SSS),
∴∠EOF=∠HOF=45°;
②连接OC,
∵∠ECO=∠EOF=∠OAF=45°,∠EOC=∠AFO,
∴△COE∽△AFO,
∴
| AF |
| CO |
| OF |
| OE |
| OA |
| CE |
∴
| AF |
| CO |
| OA |
| CE |
| OF |
| OE |
| OF |
| OE |
∴
| AF |
| CE |
| OF |
| OE |
2
| ||
| 3 |
| 8 |
| 9 |
看了(1)如图1,△ABC中,∠C...的网友还看了以下:
设函数f(x)在x=a的某个邻域内有定义,则f(x)在x=a处可导的一个充分条件是?请写出分析过程! 2020-03-30 …
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
已知函数f(x)=x/(2*x+1),数列{an}满足a[1]=1/2,a[n+1]=f(a[n] 2020-05-13 …
设F(x)=(f(x)-f(a))/(x-a),(x>a)其中f(x)在[a,+∞)上连续,f'' 2020-06-16 …
一、已知数集M满足条件:若a∈M,则(1+a)/(1-a)∈M(a≠0,a≠±1)(1)若3∈M, 2020-07-30 …
已知f(x)在点a的邻域内有定义,且limx→a{f(x)-f(a)}/(x-a)^2=c≠0,证 2020-07-31 …
已知α是第三象限角且f(α),且f(a)=sin(π-a)cos(2π-a)tan(-a+2π)/ 2020-08-03 …
F=A+A×(1+i)+…+A×(1+i)n-1,(1)等式两边同乘以(1+i):F(1+i)=A( 2020-11-01 …
函数f[x]=logaXa大于0,且a不等于1,在2,3上最大值为1,则a=当a大于1时,f(x)图 2021-01-15 …
求函数定义域呵呵!以前的都忘了!一、y=f(x-1)+f(x+1),f(u)的定义域为(0,3)二、 2021-01-31 …