早教吧作业答案频道 -->数学-->
如图,∠ABC=90°,D、E分别在BC,AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.(1)求证:△AFM≌△DFC;(2)AD与MC垂直吗?并说明理由.
题目详情
如图,∠ABC=90°,D、E分别在BC,AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
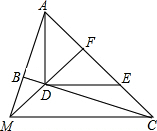
(1)求证:△AFM≌△DFC;
(2)AD与MC垂直吗?并说明理由.

(1)求证:△AFM≌△DFC;
(2)AD与MC垂直吗?并说明理由.
▼优质解答
答案和解析
证明:(1)∵AD⊥DE,AD=DE ,点F是AE的中点,
,点F是AE的中点,
∴∠AFM=∠DFC=90°,AF=DF,∠DEA=∠DAE=45°.
∵∠ABC=∠AFM=90°,
∴∠AMF+∠MAC=90°,∠DCF+∠MAC=90°,
∴∠AMF=∠DCF.
在△AFM和△DFC中,
∴△AFM≌△DFC;
(2)AD⊥MC.
理由如下:
由(1)知,△AFM≌△DFC,
∴FM=FC.
∴△FMC是等腰直角三角形,
∴∠FCM=45°.
∵∠FED=45°,
∴∠FED=∠FCM,
∴DE∥MC.
∵AD⊥DE,
∴AD⊥MC.
 ,点F是AE的中点,
,点F是AE的中点,∴∠AFM=∠DFC=90°,AF=DF,∠DEA=∠DAE=45°.
∵∠ABC=∠AFM=90°,
∴∠AMF+∠MAC=90°,∠DCF+∠MAC=90°,
∴∠AMF=∠DCF.
在△AFM和△DFC中,
|
∴△AFM≌△DFC;
(2)AD⊥MC.
理由如下:
由(1)知,△AFM≌△DFC,
∴FM=FC.
∴△FMC是等腰直角三角形,
∴∠FCM=45°.
∵∠FED=45°,
∴∠FED=∠FCM,
∴DE∥MC.
∵AD⊥DE,
∴AD⊥MC.
看了 如图,∠ABC=90°,D、...的网友还看了以下:
如图①,△ABC内接于⊙O,且∠ABC=∠C,点D在弧BC上运动.过点D作DE∥BC,DE交直线A 2020-05-13 …
一道几何证明求解.看图.无需理由.如图,在△ABC中,∠ABC=90°,AC=BC,DE为过C点的 2020-05-16 …
三角形abc中,角acb=90°,d是bc上的点,de⊥ab于点e,且dc=de,ad与ce交于点 2020-05-17 …
已知,如图,过△ABC的顶点A,作AF⊥AB且AF=AB,使AH=AC,连接BH、CF,且BH与C 2020-06-27 …
在三角形ABC中角A的外角的二等分线AD和BC的延长线相交于D点,求证,BD比DC等于AB比AC《 2020-07-02 …
已知,在三角形ABC中,角C等于90度,CH垂直AB,AT平分角CAB,交CH于D点,DE平行AB 2020-07-11 …
已知BD为三角形ABC的角平分线,CD为三角形外角角ACE的角平分线,且与BD交与D点,求证:角A 2020-07-21 …
AB是圆O直径,F.C是圆O上的两点,且弧BC=弧CF,过C点作DE垂直于AF的延长线于E点交AB 2020-07-29 …
已知三角形ABC为不等边三角形,AD⊥BC于D点,求证:D点到AB、AC边的距离必不相等用反证法 2020-08-01 …
初一几何等边三角形的求证ABC为等边三角形,顺延AB延伸至E点,从E点延伸至AC边交于D点,DE交B 2021-01-02 …