早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,P为AD上一点,连接BP,CP,过C作CE⊥BP于点E,连接ED交PC于点F.(1)求证:△ABP∽△ECB;(2)若点E恰好为BP的中点,且AB=3,AP=k(0<k<3).①求PFPC的值(用含k的代数
题目详情
如图,在矩形ABCD中,P为AD上一点,连接BP,CP,过C作CE⊥BP于点E,连接ED交PC于点F.
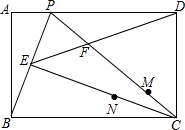
(1)求证:△ABP∽△ECB;
(2)若点E恰好为BP的中点,且AB=3,AP=k(0<k<3).
①求
的值(用含k的代数式表示);
②若M、N分别为PC,EC上的任意两点,连接NF,NM,当k=
时,求NF+NM的最小值.

(1)求证:△ABP∽△ECB;
(2)若点E恰好为BP的中点,且AB=3,AP=k(0<k<3).
①求
| PF |
| PC |
②若M、N分别为PC,EC上的任意两点,连接NF,NM,当k=
| 2 |
▼优质解答
答案和解析
(1)证明:在矩形ABCD中,∵∠A=∠ABC=90°,∵CE⊥BP,∴∠CEB=90°,∴∠A=∠CEB,∴∠APB+∠ABP=∠ABP+∠PBC=90°,∴∠APB=∠PBC,∴△ABP∽△ECB;(2) ①∵△ABP∽△ECB,∴APAB=BEBC,∵BP=9+k2,E为BP的中...
看了如图,在矩形ABCD中,P为A...的网友还看了以下:
高二不等式比较大小已知f(x)=(1+√(1+x))/x,a、b是两个不相等的实数,则下列不等式正 2020-04-26 …
设f(x)在[a,b]上可微,0小于a小于b.证明:在(a,b)内至少存在一点n.使得f(b)-f 2020-04-26 …
已知f(X)=Lg1-X/1+X,a,b属于(-1,1)求证:f(a)+f(B)=F(A+B)/1 2020-05-22 …
关于拉格朗日中值定理两个前提条件:f(x)在[a,b]上连续,在(a,b)上可导.若[a,b]换成 2020-06-22 …
已知f(x)在区间(﹣∞,+∞)上是减函数,a,b∈R,且a+b≤0,则下列正确的是?A.f(a) 2020-07-14 …
若函数f(x)是定义在R上的奇函数,且对任意正数a、b都有满足f(a+b)=f(a)*f(b),试 2020-07-15 …
已知函数fx是r上的增函数,对于实数ab若a+b>0,则()a.f(a)+f(b)>f(-a)+f 2020-07-27 …
设函数f(x)在[a,b]上连续,在(a,b)上可导且f'(x)≠0那么下列一定成立的是()A.f( 2020-11-03 …
关于泰勒公示展开求证:已知f(x)在[a,b]存在二阶导数,f'(a)=f'(b)=0,则在存在c∈ 2020-11-23 …
已知f(x)在R上是增函已知f(x)在R上是增函数,a,b∈R,且a+b≤0,则有[]A、f(a)+ 2020-12-08 …