早教吧作业答案频道 -->数学-->
如图,点F是CD的中点,且AF⊥CD,BC=ED,∠BCD=∠EDC.(1)求证:BF=EF;(2)求证:AB=AE.
题目详情
如图,点F是CD 的中点,且AF⊥CD,BC=ED,∠BCD=∠EDC.
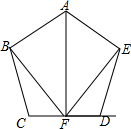
(1)求证:BF=EF;
(2)求证:AB=AE.

(1)求证:BF=EF;
(2)求证:AB=AE.
▼优质解答
答案和解析
证明:(1)∵点F是CD 的中点,
∴CF=DF,
在△BCF和△EDF中
,
∴△BCF≌△EDF(SAS),
∴FB=FE;
(2)∵△BCF≌△EDF,
∴FB=EF,∠BFC=∠EFD,
∵AF⊥CD,
∴∠BFC+∠AFB=∠AFE+∠EFD,
∴∠BFA=∠EFA,
在△ABF和△AEF中
,
∴△ABF≌△AEF(SAS),
∴AB=AE.
∴CF=DF,
在△BCF和△EDF中
|
∴△BCF≌△EDF(SAS),
∴FB=FE;
(2)∵△BCF≌△EDF,
∴FB=EF,∠BFC=∠EFD,
∵AF⊥CD,
∴∠BFC+∠AFB=∠AFE+∠EFD,
∴∠BFA=∠EFA,
在△ABF和△AEF中
|
∴△ABF≌△AEF(SAS),
∴AB=AE.
看了如图,点F是CD的中点,且AF...的网友还看了以下:
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=ax-1,其中a>0,a≠1.(1)求f( 2020-06-09 …
设f(x)=loga(x-2a)+loga(x-3a),其中a>0且a≠1.(1)已知f(4a)= 2020-06-12 …
已知:a、b为实数,关于x的方程x2-(a-1)x+b+3=0的一个实根为a+1.(1)用含a的代 2020-06-22 …
设方程|ax-1|=x的解集为A,若A⊂≠[0,2],则实数a的取值范围是a=-1或-12≤a≤1 2020-07-07 …
设A为n阶矩阵.若存在正整数m使Am=O,则称A为n阶幂零矩阵.现设A为n阶幂零矩阵,E为n阶单位 2020-07-22 …
已知函数f(x)=ax,g(x)=a2x+m,其中m>0,a>0且a≠1.当x∈[-1,1]时,y 2020-07-26 …
已知a是任意有理数,在下面各题中结论正确的个数是()①方程ax=0的解是x=1;②方程ax=a的解 2020-08-02 …
设A=I-ξξT,其中I是n阶单位矩阵,ξ是n维非零列向量,ξT是ξ的转置.证明(1)A2=A的充分 2020-11-03 …
设常数a∈R,集合A={x|(x-1)(x-a)≥0},B={x|x≥a-1}.(1)若0∈A∩B, 2020-11-06 …
已知a是任意有理数,在下面各题中结论正确的个数是()①方程ax=0的解是x=1;②方程ax=a的解是 2020-12-13 …