早教吧作业答案频道 -->数学-->
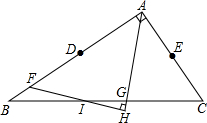
已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI.
题目详情
已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI.

▼优质解答
答案和解析
证明:延长FH交AC的延长线于点M,作CN∥AB,交FM于点N,
∵AG是∠BAC的角平分线,FH⊥AG,
∴∠FAH=∠MAH,∠AHF=∠AHM=90°,
在△AFH和△AFM中,
,
∴△AFH≌△AFM,
∴∠M=∠AFH,AF=AM,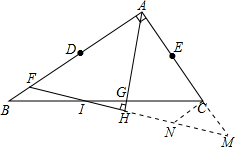
∵CN∥AB,
∴∠CNM=∠AFH,∠B=∠ICN,
∴∠CNM=∠M,
∴CM=CN,
∵CM=AM-AC=AF-AC=AD+DF-AE-EC,DF=AE,
∴CM=AD-EC
∵BF=AB-AF=2AD-AD-DF=AD-DF,DF=CE,
∴BF=CN=CM,
在△BFI和△CIN中,
,
∴△BFI≌△CIN,
∴BI=CI.
∵AG是∠BAC的角平分线,FH⊥AG,
∴∠FAH=∠MAH,∠AHF=∠AHM=90°,
在△AFH和△AFM中,
|
∴△AFH≌△AFM,
∴∠M=∠AFH,AF=AM,

∵CN∥AB,
∴∠CNM=∠AFH,∠B=∠ICN,
∴∠CNM=∠M,
∴CM=CN,
∵CM=AM-AC=AF-AC=AD+DF-AE-EC,DF=AE,
∴CM=AD-EC
∵BF=AB-AF=2AD-AD-DF=AD-DF,DF=CE,
∴BF=CN=CM,
在△BFI和△CIN中,
|
∴△BFI≌△CIN,
∴BI=CI.
看了已知:△ABC中,D是AB的中...的网友还看了以下:
证明lim(h→0)[f(x0+h)+f(x0-h)-2f(x0)]/h^2=f’’(x0)已知f 2020-05-17 …
变限积分求道问题对函数f(t+h)-f(t-h)在[-h,h]上的积分对h求导.F(h)=∫[-h 2020-05-23 …
f(x)在x=a的某个领域内有定义,则f(x)在x=a处可导的一个充分条件是()Alim[f(a+ 2020-06-18 …
求证E,F,G,M,N,H六点共面已知正方体ABCD-A1B1C1D1中,点E,F,G,H,M,N 2020-07-09 …
已知如图四边形abcd中,E,F,G,H分别是AB丶BC丶CD丶DA的中点……已知如图四边形abc 2020-07-13 …
导数乘法证明中h是什么意思?(f(x)g(x))'=lim(h→0)[f(x+h)g(x+h)-f 2020-07-22 …
高中数学问题已知f(x)在x=a处可导,求下列极限lim(x→a)[f(x)-f(a)]/(a-x) 2020-11-01 …
高二数学高手进一.(1)已知f(x)在x=x0处的导数为A,,求lim△x→0〔f(x0-2△x)- 2020-11-01 …
求导不同思路引起的不同结果习题:设f(x)的二阶导数存在,求lim[f(x+2h)-2f(x+h)+ 2020-11-03 …
若方程(3/x-2)+1=2a/x-2无解,则a=.在1/u+1/v=1/f中,已知u、v,且u+v 2021-01-22 …