早教吧作业答案频道 -->数学-->
在△ABC中,(1)如图1,BP为△ABC的角平分线,PM⊥AB于M,PN⊥BC于N,AB=50,BC=60请补全图形,并直接写出△ABP与△BPC面积的比值;(2)如图2,分别以△ABC的边AB、AC为边向外作等边三角形ABD和A
题目详情
在△ABC中,
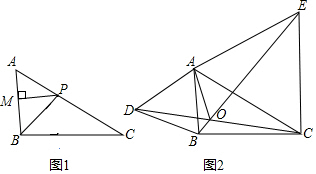
(1)如图1,BP为△ABC的角平分线,PM⊥AB于M,PN⊥BC于N,AB=50,BC=60请补全图形,并直接写出△ABP与△BPC面积的比值;
(2)如图2,分别以△ABC的边AB、AC为边向外作等边三角形ABD和ACE,CD与BE 相交于点O,求证:BE=CD;
(3)在(2)的条件下判断∠AOD与∠AOE的数量关系.(不需证明)

(1)如图1,BP为△ABC的角平分线,PM⊥AB于M,PN⊥BC于N,AB=50,BC=60请补全图形,并直接写出△ABP与△BPC面积的比值;
(2)如图2,分别以△ABC的边AB、AC为边向外作等边三角形ABD和ACE,CD与BE 相交于点O,求证:BE=CD;
(3)在(2)的条件下判断∠AOD与∠AOE的数量关系.(不需证明)
▼优质解答
答案和解析
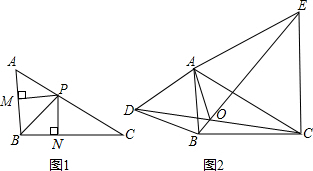 (1)如图1,作PN⊥BC于N,
(1)如图1,作PN⊥BC于N,
又∵BP为△ABC的角平分线,PM⊥AB于M,
∴PM=PN,
∴S△ABP:S△BPC=(
AB•PM):(
BC•PN)=AB:BC,
∵AB=50,BC=60,
∴△ABP与△BPC面积的比值为
;
(2)证明:如图2,∵△ABD和△ACE都是等边三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△ABE和△ADC中,
,
∴△ABE≌△ADC(SAS),
∴BE=CD;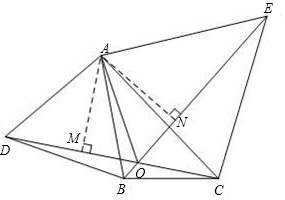
(3)∠AOD与∠AOE的数量关系为:∠AOD=∠AOE.
理由:如图,过点A作AM⊥DC于M,作AN⊥BE于N,
由(2)可得,△DAC≌△BAE,且DC=BE,
∴S△DAC=S△BAE,
即
×CD×AM=
×BE×AN,
∴AM=AN,
∴点A在∠DOE的角平分线上,
∴∠AOD=∠AOE.
 (1)如图1,作PN⊥BC于N,
(1)如图1,作PN⊥BC于N,又∵BP为△ABC的角平分线,PM⊥AB于M,
∴PM=PN,
∴S△ABP:S△BPC=(
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=50,BC=60,
∴△ABP与△BPC面积的比值为
| 5 |
| 6 |
(2)证明:如图2,∵△ABD和△ACE都是等边三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△ABE和△ADC中,
|
∴△ABE≌△ADC(SAS),
∴BE=CD;

(3)∠AOD与∠AOE的数量关系为:∠AOD=∠AOE.
理由:如图,过点A作AM⊥DC于M,作AN⊥BE于N,
由(2)可得,△DAC≌△BAE,且DC=BE,
∴S△DAC=S△BAE,
即
| 1 |
| 2 |
| 1 |
| 2 |
∴AM=AN,
∴点A在∠DOE的角平分线上,
∴∠AOD=∠AOE.
看了在△ABC中,(1)如图1,B...的网友还看了以下:
如图,点A(m,m+1),B(m+3,m-1)都在反比例函数y=x分之k的图像上.(1)会的(2) 2020-04-08 …
将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC 2020-05-17 …
如图,点A(m,m+1),B(m+3,m-1)都在反比例函数y=kx的图象上.(1)求m,k的值; 2020-06-11 …
如图,点A(m,m+1),B(m+3,m-1)都在反比例函数y=kx的图象上.(1)求m,k的值; 2020-06-12 …
如图,边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上,则△AEF的内切圆半径为( 2020-06-15 …
如图,边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上,则△AEF的内切圆半径为( 2020-06-29 …
如图,点A(m,m+1),B(m+3,m-1)都在反比例函数y=k/x的图像上如果M为x轴上一点, 2020-06-29 …
对a,b定义一种新运算M,规定M(a,b)=2aba-b,这里等式右边是通常的四则运算,例如:M( 2020-07-06 …
在Rt△ABC中,∠C=90°,AC=6,AB=10,⊙B的半径长为1,⊙B交边CB于点P,点O是 2020-07-20 …
如果M边形与N边形的内角和的差为540°,那么M-N的值为? 2021-02-21 …