早教吧作业答案频道 -->数学-->
(1)如图1,△ABC和△DEF都是边长为2的等边三角形,O是BC和EF的中点,连接CF,判断CF与AD的位置关系和数量关系.(2)如图2,设直线CF与直线AD的交点为G,将△DEF绕点O旋转,在旋转过程中,
题目详情
(1)如图1,△ABC和△DEF都是边长为2的等边三角形,O是BC和EF的中点,连接CF,判断CF与AD的位置关系和数量关系.
(2)如图2,设直线CF与直线AD的交点为G,将△DEF绕点O旋转,在旋转过程中,EG的最大值为___.
(2)如图2,设直线CF与直线AD的交点为G,将△DEF绕点O旋转,在旋转过程中,EG的最大值为___.

▼优质解答
答案和解析
(1)如图1中,结论:CF⊥AD,AD=
CF;
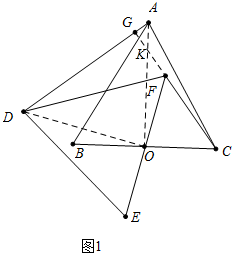
理由:连接AO、DO、延长CF交AD于G,如图1.
∵△ABC,△EFD均是边长为2的等边三角形,点D是边BC、EF的中点,
∴AO⊥BC,DO⊥EF,AO=DO,CO=OF,
∴∠AOD=90°-∠AOF=∠COF,
=
,
∴△ADO∽△COF,
∴∠OAD=∠OCF,
=
=
,
∵∠AKG=∠FKO,∠FCO+∠FKO=90°,
∴∠KAG+∠AKG=90°,
∴∠AGF90°,
∴AD⊥CF,
∴CF⊥AD,AD=
CF;
(2)如图2中,设DF的中点为M.连接EM、GM.
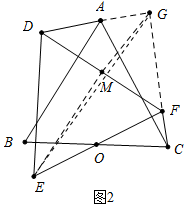
∵CF⊥AD,
∴∠DGF=90°,
∴点G在以DF为直径的圆上,
∵EG<EM+GM,
∴当E、M、G共线时,EG=EM+MG的值最大,
∵EM=DE•sin60°=
,GM=
DF=1,
∴EG的最大值为
+1.
| 3 |

理由:连接AO、DO、延长CF交AD于G,如图1.
∵△ABC,△EFD均是边长为2的等边三角形,点D是边BC、EF的中点,
∴AO⊥BC,DO⊥EF,AO=DO,CO=OF,
∴∠AOD=90°-∠AOF=∠COF,
| AO |
| CO |
| OD |
| OF |
∴△ADO∽△COF,
∴∠OAD=∠OCF,
| CF |
| AD |
| OC |
| AO |
| ||
| 3 |
∵∠AKG=∠FKO,∠FCO+∠FKO=90°,
∴∠KAG+∠AKG=90°,
∴∠AGF90°,
∴AD⊥CF,
∴CF⊥AD,AD=
| 3 |
(2)如图2中,设DF的中点为M.连接EM、GM.

∵CF⊥AD,
∴∠DGF=90°,
∴点G在以DF为直径的圆上,
∵EG<EM+GM,
∴当E、M、G共线时,EG=EM+MG的值最大,
∵EM=DE•sin60°=
| 3 |
| 1 |
| 2 |
∴EG的最大值为
| 3 |
看了(1)如图1,△ABC和△DE...的网友还看了以下:
若点O是平行四边形ABCD对角线AC的中点,EF⊥AC于O,交AD、BC分别于E、F,那么线段DE 2020-05-16 …
向量a=(sino,coso)与向量b=(根号3,1),其中o∈(0,π/2).(1)若向量a与向 2020-05-17 …
已知动直线l过点P(4,0).交抛物线y^2=2mx(m>0)于A,B两点,O为原点,Q是P关于O 2020-06-07 …
(2011•上海模拟)如图所示,一半径为R的均匀带正电圆环水平放置,环心为O点,质量为m的带正电的 2020-07-14 …
如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a﹣b|=3,|b﹣c|=5,且原点O与A 2020-07-30 …
如图所示,在真空中有两个固定的等量异种点电荷+Q和-Q.直线MN是两点电荷连线的中垂线,O是两点电荷 2020-12-05 …
高中数学函数已知函数f(x)对一切实数x,y都有f(x+y)-f(y)=x(x+2y+1)成立;且f 2020-12-08 …
如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a-b|=3,|b-c|=5,且原点O与A、 2020-12-14 …
如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部 2021-01-13 …
读图(沿40°N亚洲东西向地形剖面图),有关F地的说法正确的是()A、该地有丰富的石油和铁矿资源B、 2021-01-14 …