早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.(1)若BE=22,AE=3,求AF的长;(2)若∠BAC=∠DAF,求证:2AF=AD;(3)请直接写出线段AD、BE、AE
题目详情
如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
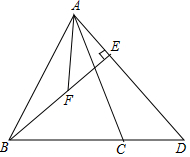
(1)若BE=2
,AE=
,求AF的长;
(2)若∠BAC=∠DAF,求证:2AF=AD;
(3)请直接写出线段AD、BE、AE的数量关系.

(1)若BE=2
| 2 |
| 3 |
(2)若∠BAC=∠DAF,求证:2AF=AD;
(3)请直接写出线段AD、BE、AE的数量关系.
▼优质解答
答案和解析
(1)∵BE的中点是F,BE=2
,
∴EF=
,
∵AE=
,BE⊥AD,
∴AF=
=
,
(2)如图,延长AF至M点,使AF=MF,连接BM,
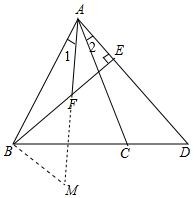
在△AEF和△MBF中,
∴△AEF≌△MFB(SAS),
∴∠FAE=∠FMB,
∴AE∥MB,
∴∠EAB+∠ABM=180°,
又∵AB=AC,DB=DA,
∴∠ABC=∠ACB=∠BAD,
∴∠ACD=180°-∠ACB,∠ABM=180°-∠BAD,
∴∠ACD=∠ABM.又∵∠BAC=∠DAF,
∴∠1=∠2.
在△ABM和△ACD中,
,
∴△ABM≌△ACD,
∴AM=AD,
∴2AF=AD
(3)结论:AD2=BE2=(AD-AE)2.
理由∵DB=DA,BE⊥AD,
∴BD2=BE2+DE2,
∴AD2=BE2=(AD-AE)2.
| 2 |
∴EF=
| 2 |
∵AE=
| 3 |
∴AF=
| AE2+EF2 |
| 5 |
(2)如图,延长AF至M点,使AF=MF,连接BM,

在△AEF和△MBF中,
|
∴△AEF≌△MFB(SAS),
∴∠FAE=∠FMB,
∴AE∥MB,
∴∠EAB+∠ABM=180°,
又∵AB=AC,DB=DA,
∴∠ABC=∠ACB=∠BAD,
∴∠ACD=180°-∠ACB,∠ABM=180°-∠BAD,
∴∠ACD=∠ABM.又∵∠BAC=∠DAF,
∴∠1=∠2.
在△ABM和△ACD中,
|
∴△ABM≌△ACD,
∴AM=AD,
∴2AF=AD
(3)结论:AD2=BE2=(AD-AE)2.
理由∵DB=DA,BE⊥AD,
∴BD2=BE2+DE2,
∴AD2=BE2=(AD-AE)2.
看了如图,在△ABC中,AB=AC...的网友还看了以下:
如图,已知三角形abc中,ac=4,bc=3,ab=5.现绕ac边所以的直线旋转一周,求旋转后的几 2020-06-05 …
(2014•常德)如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一 2020-06-12 …
如图,在△ABC中,AB=AC,cosB=1/3,BC=2,点D,E,F分别在AC,AB,BC边上 2020-06-27 …
(2000•荆门)如图,以Rt△ABC的直角边BC为直径画半圆,交斜边AB于D,若AC=233,B 2020-07-19 …
如图,以Rt△ABC的直角边BC为直径画半圆,交斜边AB于D,若AC=233,BD=3,求图中阴影 2020-07-19 …
一个数学小问题在直线L上取A,B两点,使AB=12厘米,再在直线L上取一点C,使AC:BC=3:1 2020-07-26 …
(1)A为直线a外一点,B是直线a上一点,点A到直线a的距离为3厘米,则线段AB的长度的取值范围是 2020-08-01 …
如图,等腰直角三角形ABC中,AB=AC=2cm,P在BC上,以C为圆心、PC为半径画弧交边AC于 2020-08-03 …
(2005•宜宾)已知△ABC中,AB=3,BC=4,则第三边AC的取值范围是()A.3<AC<4B 2020-11-12 …
已知直线y=-43x+4与x轴和y轴分别交与A、B两点,另一直线过点A和点C(7,3).(1)求直线 2021-01-10 …