早教吧作业答案频道 -->数学-->
四边形ABCD是菱形,点E在BC上,点F在AB上,点H在CD上,连接AE,FH交于点P,∠APF=∠ABC.(1)如图1,若∠ABC=90°,点F和点B重合,求证:AE=BH;(2)如图2.求证:AE=FH;(3)如图3,若AF+CH=BE,
题目详情
四边形ABCD是菱形,点E在BC上,点F在AB上,点H在CD上,连接AE,FH交于点P,∠APF=∠ABC.
(1)如图1,若∠ABC=90°,点F和点B重合,求证:AE=BH;
(2)如图2.求证:AE=FH;
(3)如图3,若AF+CH=BE,求∠B的度数.
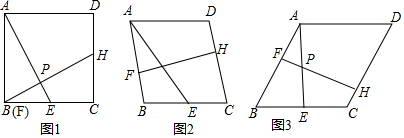
(1)如图1,若∠ABC=90°,点F和点B重合,求证:AE=BH;
(2)如图2.求证:AE=FH;
(3)如图3,若AF+CH=BE,求∠B的度数.

▼优质解答
答案和解析
(1)证明:如图1中,
∵四边形ABCD是菱形,∠ABC=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∵∠APF=∠ABC=90°,
∴∠BAE+∠ABP=90°,∠ABP+∠CBH=90
∴∠BAE=∠CBH,
在△ABE和△BCH中,
,
∴△ABE≌△BCH,
∴AE=BH.
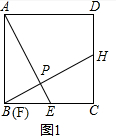
(2)证明:如图2中,延长CB到N,使得AN=AE,作HM∥BC交AB于M.
则四边形ADHM是平行四边形,AD=HM,
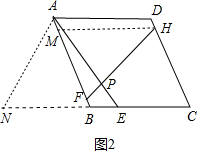
∵四边形ABCD是菱形,
∴AB=AD=HM,
∵HM∥CN,
∴∠HMF=∠ABN,
∵∠APF=∠ABC,∠PAF=∠BAE,
∴∠AFP=∠AEB=∠N,
∴△ABN≌△HMF,
∴AN=HF,
∵AE=AN,
∴AE=HF.
(3) 如图3中,在CB取一点N,使得AN=AE,作FM∥BC交CD于M.
则四边形ADMF是平行四边形,AD=FM,AF=DM,
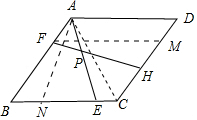
由(1)可知△ABN≌△FMH,
BN=HM,
∵BC=CD,AF+CH=DM+CH=BE,
∴CE=HM=BN,
在△ANB和△AEC中,
,
∴△ANB≌△AEC,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠B=60°.

∵四边形ABCD是菱形,∠ABC=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∵∠APF=∠ABC=90°,
∴∠BAE+∠ABP=90°,∠ABP+∠CBH=90
∴∠BAE=∠CBH,
在△ABE和△BCH中,
|
∴△ABE≌△BCH,
∴AE=BH.
(2)证明:如图2中,延长CB到N,使得AN=AE,作HM∥BC交AB于M.
则四边形ADHM是平行四边形,AD=HM,

∵四边形ABCD是菱形,
∴AB=AD=HM,
∵HM∥CN,
∴∠HMF=∠ABN,
∵∠APF=∠ABC,∠PAF=∠BAE,
∴∠AFP=∠AEB=∠N,
∴△ABN≌△HMF,
∴AN=HF,
∵AE=AN,
∴AE=HF.
(3) 如图3中,在CB取一点N,使得AN=AE,作FM∥BC交CD于M.
则四边形ADMF是平行四边形,AD=FM,AF=DM,

由(1)可知△ABN≌△FMH,
BN=HM,
∵BC=CD,AF+CH=DM+CH=BE,
∴CE=HM=BN,
在△ANB和△AEC中,
|
∴△ANB≌△AEC,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠B=60°.
看了四边形ABCD是菱形,点E在B...的网友还看了以下:
在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形,点P为B 2020-04-26 …
在锐角三角形ABC中,已知AB>AC,P是BC边上任意一点,点P关于AB的对称点为E(看下文)关于 2020-05-20 …
抛物线Y=-X²+2X+3与X轴相交于点A,B两点(点A在点B左侧),与Y轴交于点C,顶点为D.连 2020-06-02 …
已知椭圆C1:x216+y215=1的左焦点为F,点P为椭圆上一动点,过点P向以F为圆心,1为半径 2020-07-19 …
如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停 2020-07-21 …
(2007•青浦区二模)如图,⊙A和⊙B是外离的两圆,两圆的连心线分别交⊙A、⊙B于E、F,点P是 2020-07-31 …
已知抛物线C:y2=2px(p>0)的焦点为F,点P在C上且其横坐标为1,以F为圆心,|FP|为半 2020-07-31 …
还是初三几何题一正方形ABCD的边长为4,E是BC边上的中点,点P在射线AD上.过P作PE⊥AE于F 2020-11-03 …
(2009•滨州一模)已知P点在曲线F:y=x3-x上,且曲线F在点P处的切线与直线x+2y=0垂直 2020-11-13 …
初三的数学题目,帮帮忙如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF 2021-01-11 …