早教吧作业答案频道 -->数学-->
如图,在平行四边形ABCD中,AB=6,BC=10,对角线AC⊥AB,点E、F分别是BC,AD上的点,且BE=DF.(1)求证:四边形AECF是平行四边形.(2)①当BE长度为时,四边形AECF是菱形.②当BE长度为时
题目详情
如图,在平行四边形ABCD中,AB=6,BC=10,对角线AC⊥AB,点E、F分别是BC,AD上的点,且BE=DF.
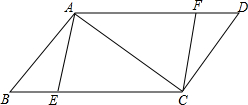
(1)求证:四边形AECF是平行四边形.
(2)①当BE长度为___时,四边形AECF是菱形.
②当BE长度为___时,四边形AECF是矩形.
(3)求平行四边形ABCD的面积.

(1)求证:四边形AECF是平行四边形.
(2)①当BE长度为___时,四边形AECF是菱形.
②当BE长度为___时,四边形AECF是矩形.
(3)求平行四边形ABCD的面积.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形;
(2) ①∵四边形AECF是菱形,
∴AE=CE,
∴∠EAC=∠ECA,
∵AC⊥AB,
∴∠BAC=90°,
∴∠B+∠ECA=90°,∠BAE+∠EAC=90°,
∴∠B=∠BAE,
∴AE=BE,
∴BE=CE=
BC=5;
故答案为:5;
②∵四边形AECF是矩形,
∴∠AEC=90°,
∴∠AEB=90°=∠BAC,
∵∠B=∠B,
∴△ABE∽△CBA,
∴
=
,
∴BE=
=
=3.6;
故答案为:3.6;
(3) ∵AC⊥AB,
∴AC=
=
=8,
∴平行四边形ABCD的面积=AB•AC=6×8=48.
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形;
(2) ①∵四边形AECF是菱形,
∴AE=CE,
∴∠EAC=∠ECA,
∵AC⊥AB,
∴∠BAC=90°,
∴∠B+∠ECA=90°,∠BAE+∠EAC=90°,
∴∠B=∠BAE,
∴AE=BE,
∴BE=CE=
| 1 |
| 2 |
故答案为:5;
②∵四边形AECF是矩形,
∴∠AEC=90°,
∴∠AEB=90°=∠BAC,
∵∠B=∠B,
∴△ABE∽△CBA,
∴
| AB |
| BC |
| BE |
| AB |
∴BE=
| AB2 |
| BC |
| 62 |
| 10 |
故答案为:3.6;
(3) ∵AC⊥AB,
∴AC=
| BC2-AB2 |
| 102-62 |
∴平行四边形ABCD的面积=AB•AC=6×8=48.
看了 如图,在平行四边形ABCD中...的网友还看了以下:
向量组证明问题设A,B分别为m*r,r*n阶矩阵,且AB=0,求证(1)B的各列向量是齐次线性方程 2020-05-14 …
如图,梯形ABCD中,AD∥BC,G,E分别是AB,CD中点,连接AE,GF.求证:(1)四边形A 2020-05-16 …
角A30°,角B+C=150°,a边为1,b边为根号3,求三角形ABC的面积 2020-05-22 …
已知梯形ABCD,AD平行BC,对角线AC,BD相交於点O,A',B',C',D'分别是AO,BO 2020-06-07 …
四边形ADCDAB=DCAC=BDAD不等于BCAB平行DE(E在BC上)求证1四边形ABED平行 2020-07-23 …
已知a>0.b>0且a+b>2,求证1+b/a,1+a/b中至少有一个少于2是(1+b)/a~(1 2020-07-25 …
已知a的平方,b的平方,c的平方是一个等差数列,求证1/b+c,1/a+c,1/a+b也是等差数列 2020-07-28 …
已知a,b是正数,且a+b=1,求证1/b+1/a≥4 2020-07-30 …
正弦定理的题在△ABC中,已知A、B、C成等差数列且sinA×sinC=cos²B,S△=4√3, 2020-08-02 …
设二次函数f(x)=x^2+bx+c(b,c属于R),已知不论m,n为何实数,恒有f(sinm)大于 2020-12-08 …