早教吧作业答案频道 -->数学-->
如图,点P是菱形ABCD对角线AC上一个动点,PE⊥AD,PF⊥CD.(1)当点P在线段AC上运动时,PE+PF的值是一个定值吗?请说明理由.(2)当点P在线段AC的延长线上运动时,PE与PF的长度满足什么样
题目详情
如图,点P是菱形ABCD对角线AC上一个动点,PE⊥AD,PF⊥CD.
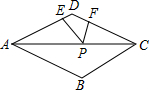
(1)当点P在线段AC上运动时,PE+PF的值是一个定值吗?请说明理由.
(2)当点P在线段AC的延长线上运动时,PE与PF的长度满足什么样的关系式?

(1)当点P在线段AC上运动时,PE+PF的值是一个定值吗?请说明理由.
(2)当点P在线段AC的延长线上运动时,PE与PF的长度满足什么样的关系式?
▼优质解答
答案和解析
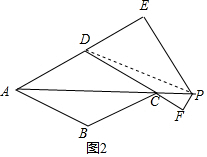
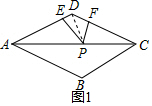 (1)是定值,证明:连接DP,设△ACE的边AD上的高为h,
(1)是定值,证明:连接DP,设△ACE的边AD上的高为h,
∵菱形ABCD,
∴DA=DC,
∵PE⊥AD,PF⊥CD,
∴△ACD的面积=△ADP的面积+△CDP的面积=
AD•PE+
CD•PF=
AD(PE+PF),
∵△ACD的面积=
AD•h,
∴
AD(PE+PF)=
AD•h,
∴PE+PF=h(定值),
即PE+PF等于等腰三角形ACD的腰AD上的高;
(2)满足PE-PF等于等腰三角形ACD的腰AD上的高,
证明:连接DP,设△ACE的边AD上的高为h,
∵菱形ABCD,
∴DA=DC,
∵PE⊥AD,PF⊥CD,
∴△ACD的面积=△ADP的面积-△CDP的面积=
AD•PE-
CD•PF=
AD(PE-PF),
∵△ACD的面积=
AD•h,
∴
AD(PE-PF)=
AD•h,
∴PE-PF=h(定值),
即PE-PF等于等腰三角形ACD的腰AD上的高.

 (1)是定值,证明:连接DP,设△ACE的边AD上的高为h,
(1)是定值,证明:连接DP,设△ACE的边AD上的高为h,∵菱形ABCD,
∴DA=DC,
∵PE⊥AD,PF⊥CD,
∴△ACD的面积=△ADP的面积+△CDP的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ACD的面积=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴PE+PF=h(定值),
即PE+PF等于等腰三角形ACD的腰AD上的高;
(2)满足PE-PF等于等腰三角形ACD的腰AD上的高,
证明:连接DP,设△ACE的边AD上的高为h,
∵菱形ABCD,
∴DA=DC,
∵PE⊥AD,PF⊥CD,
∴△ACD的面积=△ADP的面积-△CDP的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ACD的面积=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴PE-PF=h(定值),
即PE-PF等于等腰三角形ACD的腰AD上的高.
看了 如图,点P是菱形ABCD对角...的网友还看了以下:
1、直线y=kx+b经过点A(0,1)B(-3,0),P是这条直线上的一动点,以P为圆心的圆切x轴 2020-06-03 …
已知直线y=12x与y=kx(k>0)交于A、B两点,且点A的横坐标为4,过原点O的另一条直线l交 2020-06-12 …
在平面直角坐标系xOy中,点P在由直线,直线和直线所围成的区域内或其边界上,点Q在x轴上,若点R的 2020-06-14 …
几何图形是由点.线.面组成的,其中点是,线分为两类.面分为两类;其中柱体分为两类.椎体分为两类; 2020-06-21 …
已只直线y=1/2x与双曲线y=k/x(k>0)交A,B2点,且A的横坐标为4求1k的值2若双曲线 2020-07-12 …
如图,已知直线y=1/2x与双曲线y=k/x(k>0)交于A.B两点,且点A的横坐标为4,过原点O 2020-08-01 …
如图所示为质点P、Q做匀速圆周运动的向心加速度随半径变化的图线。表示质点P的图线是过原点的一条直线 2020-08-01 …
几何图形都是由点,线,面,体组成的.判断这句话是否正确,为什么?请问平面图形也属于几何图形,那么能 2020-08-02 …
已知点P(x0,y0)和直线kx-y+b=0(由y=kx+b变形而得),则点P到直线kx-y+b=0 2020-11-03 …
1.如图,已知直线y=1/2x与双曲线y=k/x(k>0)交与A、B两点,且点A的横坐标为4,过原点 2021-01-10 …