早教吧作业答案频道 -->数学-->
如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.(1)求证:DC是⊙O的切线;(2)若∠CBA=30°,射线EP交⊙O于点F,当
题目详情
如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.
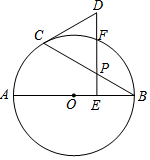
(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由.

(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
▼优质解答
答案和解析
(1)证明:连接OC,
∵DP=DC,
∴∠DPC=∠DCP,
∵∠DPC=∠BPE,
∴∠BPE=∠DCP,
∵PE⊥AB,
∴∠BEP=90°,
∴∠B+∠APE=90°,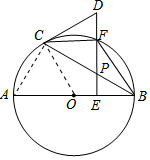
∵OB=OC,
∴∠OCB=∠B,
∴∠OCB+∠DCP=90°,
∴OC⊥CD,
∴直线CD与⊙O相切;
(2)以B、O、C、F为顶点的四边形是菱形,理由如下:
连接AC,
∵∠CBA=30°,
∴∠A=60°,
∴△OAC为等边三角形,
∴∠BOC=120°,
连接OF,BF,CF
∵F是弧BC的中点,
∴∠BOF=∠COF=60°,
∴△BOF与△COF均为等边三角形,
∴BF=BO=OC=CF,
∴四边形BOCF为菱形.
(1)证明:连接OC,
∵DP=DC,
∴∠DPC=∠DCP,
∵∠DPC=∠BPE,
∴∠BPE=∠DCP,
∵PE⊥AB,
∴∠BEP=90°,
∴∠B+∠APE=90°,

∵OB=OC,
∴∠OCB=∠B,
∴∠OCB+∠DCP=90°,
∴OC⊥CD,
∴直线CD与⊙O相切;
(2)以B、O、C、F为顶点的四边形是菱形,理由如下:
连接AC,
∵∠CBA=30°,
∴∠A=60°,
∴△OAC为等边三角形,
∴∠BOC=120°,
连接OF,BF,CF
∵F是弧BC的中点,
∴∠BOF=∠COF=60°,
∴△BOF与△COF均为等边三角形,
∴BF=BO=OC=CF,
∴四边形BOCF为菱形.
看了 如图,AB是⊙O的直径,点P...的网友还看了以下:
正方体ABCD-A'B'C'D' EF分别为AA'.CC'的中点 P是CC'上的动点 过点EDP坐 2020-05-16 …
(2014•天津一模)已知函数f(x)=ax2+1,g(x)=x3+bx,其中a>0,b>0.(Ⅰ 2020-06-08 …
已知函数f(x)=x³+3‖x-a‖(a>0),(1)当a=1时,在曲线在曲线y=f(x)上点P处 2020-06-15 …
如图,设抛物线y2=2px(p>0)的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1,(Ⅰ) 2020-06-29 …
P(X1,Y1)是直线l:f(X,Y)=0上一点,Q(X2,Y2)是l外一点,则方程f(X,Y)= 2020-07-15 …
已知函数f(x)=,(Ⅰ)求函数f(x)的单调区间和极值;(Ⅱ)设P(x1,y1),Q(x2,y2 2020-07-21 …
已知F是抛物线C:x2=4y的焦点,A(x1,y1),B(x2,y2)为抛物线C上不同的两点,l1 2020-07-31 …
已知点F(1,0)和直线l:x=-1,动点P到直线l的距离等于到点F的距离.(1)求点P的轨迹C的方 2020-11-27 …
求一个符合条件的函数.在f(x)这个函数上的任意两点(p,f(p)),(q,f(q)),所确定的这条 2020-12-08 …
初三的数学题目,帮帮忙如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF 2021-01-11 …