早教吧作业答案频道 -->数学-->
如图,在平行六面体ABCD-A1B1C1D1中,AD=1,CD=2,A1D⊥平面ABCD,AA1与底面ABCD所成角为θ(0<θ<π2),∠ADC=2θ.(1)求证:平面六面体ABCD-A1B1C1D1的体积V=4sin2θ,并求V的取值范围;(2)若θ=4
题目详情
如图,在平行六面体ABCD-A1B1C1D1中,AD=1,CD=2,A1D⊥平面ABCD,AA1与底面ABCD所成角为θ(0<θ<
),∠ADC=2θ.
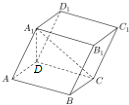
(1)求证:平面六面体ABCD-A1B1C1D1的体积V=4sin2θ,并求V的取值范围;
(2)若θ=45°,求异面直线A1C与BB1所成角的大小.
| π |
| 2 |

(1)求证:平面六面体ABCD-A1B1C1D1的体积V=4sin2θ,并求V的取值范围;
(2)若θ=45°,求异面直线A1C与BB1所成角的大小.
▼优质解答
答案和解析
证明:(1)∵A1D⊥平面ABCD,
∴∠A1AD为直线AA1与底面ABCD所成的角,即∠A1AD=θ,
∵AD=1,A1D⊥AD,∴A1D=tanθ.
∵AD=1,CD=2,∠ADC=2θ,
∴S四边形ABCD=2S△ADC=2×
×1×2×sin2θ=4sinθcosθ.
∴平面六面体ABCD-A1B1C1D1的体积V=S四边形ABCD•A1D=4sinθcosθ•tanθ=4sin2θ.
∵0<θ<
,∴0<sinθ<1,
∴0<V<4.
(2)∵AA1∥BB1,∴∠AA1C为异面直线A1C与BB1所成的角.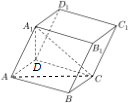
连结AC.
∵∠A1AD=45°,AD=1,A1D⊥AD,∴A1A=
,A1D=1.
∵AD=1,CD=2,∠ADC=2θ=90°,∴AC=
.
∵A1D⊥平面ABCD,CD⊂平面ABCD,∴A1D⊥CD.
∴A1C=
=
.
在△AA1C中,由余弦定理得cos∠AA1C=
=
.
∴∠AA1C=arccos
.
异面直线A1C与BB1所成角为arccos
∴∠A1AD为直线AA1与底面ABCD所成的角,即∠A1AD=θ,
∵AD=1,A1D⊥AD,∴A1D=tanθ.
∵AD=1,CD=2,∠ADC=2θ,
∴S四边形ABCD=2S△ADC=2×
| 1 |
| 2 |
∴平面六面体ABCD-A1B1C1D1的体积V=S四边形ABCD•A1D=4sinθcosθ•tanθ=4sin2θ.
∵0<θ<
| π |
| 2 |
∴0<V<4.
(2)∵AA1∥BB1,∴∠AA1C为异面直线A1C与BB1所成的角.

连结AC.
∵∠A1AD=45°,AD=1,A1D⊥AD,∴A1A=
| 2 |
∵AD=1,CD=2,∠ADC=2θ=90°,∴AC=
| 5 |
∵A1D⊥平面ABCD,CD⊂平面ABCD,∴A1D⊥CD.
∴A1C=
| A1D2+CD2 |
| 5 |
在△AA1C中,由余弦定理得cos∠AA1C=
| 2+5-5 | ||||
2×
|
| ||
| 10 |
∴∠AA1C=arccos
| ||
| 10 |
异面直线A1C与BB1所成角为arccos
|
看了 如图,在平行六面体ABCD-...的网友还看了以下:
在三角形ABC中,角ABC=60度,AB=2,BC=3,在BC上任取一点D,使三角形ABD为锐角三 2020-05-14 …
在△ABC中,a,b,c分别为内角A,B,C的对边,a^2-c^2=b^2-8bc/5,a=3,△ 2020-06-12 …
三角形问题在三角形ABC中,角A=30度,若AB=4,则角A的对边BC长的取值范围是(A)2(B) 2020-07-19 …
如图11.2-33,已知三角形ABC中,角CAB,角ABC的邻补角的平分线相交于D(1)当角C=9 2020-07-21 …
在等腰三角形ABC中,顶角B=20度,分别在BC和AC上取点D.E,使角DAC等于60度,角ECA 2020-07-22 …
已知角A.B.C.D顺次为图内接四边形的四个内角,求证:sin(A/2+D)=cos(C/2-D) 2020-07-26 …
三角函数命题正确的是A.零角是最小的角B.锐角是第一象限角C.第一象限的角是锐角D.π/2的角是第 2020-07-30 …
x^2/a^2-y^2/b^2=1(a>0b>0)的两条渐近线构成的角中,以实轴位角平分线的角记作 2020-08-01 …
三角形ABC中,角ABC=60度,AB=2,BC=5,在线段BC上任取一点D,求三角形ABD为钝角 2020-08-03 …
已知三角形ABC的角A由CB的外角平分线交角ABC的角平分线于点D,试说明角D=2/1角A的理 2020-08-03 …
 扫描下载二维码
扫描下载二维码
