早教吧作业答案频道 -->数学-->
如图,平行六面体体ABCD-A1B1C1D1中,所有棱长均为1,且∠BAD=∠A1AB=∠A1AC=60°.(Ⅰ)求证:平面A1BD⊥平面A1ACC1;(Ⅱ)求四棱锥A1-BB1D1D的体积.
题目详情
如图,平行六面体体ABCD-A1B1C1D1中,所有棱长均为1,且∠BAD=∠A1AB=∠A1AC=60°.
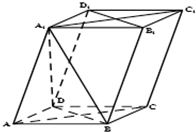
(Ⅰ)求证:平面A1BD⊥平面A1ACC1;
(Ⅱ)求四棱锥A1-BB1D1D的体积.

(Ⅰ)求证:平面A1BD⊥平面A1ACC1;
(Ⅱ)求四棱锥A1-BB1D1D的体积.
▼优质解答
答案和解析
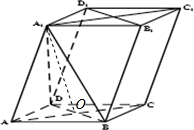 (Ⅰ)证明:连接AC、BD、A1B、A1D,AC与BD相交于一点O,连接A1O,
(Ⅰ)证明:连接AC、BD、A1B、A1D,AC与BD相交于一点O,连接A1O,
因为平行六面体ABCD-A1B1C1D1中,所有棱长均为1,
所以AC⊥BD,且O为BD中点,∠BAD=∠A1AB=∠A1AD=60°,
所以A1B=A1D=BD,所A1O⊥BD,A1O∩A1C=O,
所以BD⊥平面A1ACC1,BD⊂平面A1BD,
所以平面A1BD⊥平面A1ACC1;
(Ⅱ) 由(Ⅰ)知A1A⊥BD,又A1A∥B1B,所以B1B⊥BD,
四棱锥A1-BB1D1D为正四棱锥,V=
SBB1D1D•h,h为A1到平面BB1D1D的距离,h=
=
,SBB1D1D=1×1=1,
∴V=
.
 (Ⅰ)证明:连接AC、BD、A1B、A1D,AC与BD相交于一点O,连接A1O,
(Ⅰ)证明:连接AC、BD、A1B、A1D,AC与BD相交于一点O,连接A1O,因为平行六面体ABCD-A1B1C1D1中,所有棱长均为1,
所以AC⊥BD,且O为BD中点,∠BAD=∠A1AB=∠A1AD=60°,
所以A1B=A1D=BD,所A1O⊥BD,A1O∩A1C=O,
所以BD⊥平面A1ACC1,BD⊂平面A1BD,
所以平面A1BD⊥平面A1ACC1;
(Ⅱ) 由(Ⅰ)知A1A⊥BD,又A1A∥B1B,所以B1B⊥BD,
四棱锥A1-BB1D1D为正四棱锥,V=
| 1 |
| 3 |
(
|
| ||
| 2 |
∴V=
| ||
| 6 |
看了 如图,平行六面体体ABCD-...的网友还看了以下:
已知直线a平行平面α,直线b垂直平面α,求证a垂直b不要那些随便打几个字的~ 2020-04-05 …
物体A叠放在物体B上,B置于光滑水平面C上.A、B质量分别为5kg和15kg,加在A上的水平衡力F 2020-05-13 …
已知a,b,y是三个不同平面,求证:a//b,b//y,则a//y 2020-05-20 …
用反证法证明:已知:一点A和平面α求证:经过点A只能有一条直线和平面α垂直.如果是这样的证明方法: 2020-08-01 …
(1)用分析法证明:当一个圆和一个正方形的周长相等时,圆的面积比正方形的面积大.(2)用反证法已知 2020-08-01 …
用反证法证明:已知,在同一平面内有三条直线a,b,c,a⊥c,b⊥c.求证:a∥b.证明:假设所求 2020-08-01 …
已知a,b是异面直线,a,b∈α,c,d∈β,求证:ac,bd是异面直线.没写太明白,已知a,b是 2020-08-02 …
已知a,b为异面直线,则下列命题中正确的是()A.过a,b外一点P一定可以引一条与a,b都平行的直 2020-08-02 …
证明:三个向量a,b,c不共面,那么对于空间任一向量p,存在唯一有序实数对x,y,z,使p=xa+ 2020-08-03 …
权方和不等式的题a,b,c>0求证1111——+————+————大于等于————a(b+1)b( 2020-08-03 …