早教吧作业答案频道 -->数学-->
如图在Rt△ACB中,C为直角顶点,∠ABC=25°,O为斜边中点.将OA绕着点O逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为.
题目详情
如图在Rt△ACB中,C为直角顶点,∠ABC=25°,O为斜边中点.将OA绕着点O逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为___.


▼优质解答
答案和解析
 ∵△BCP恰为轴对称图形,
∵△BCP恰为轴对称图形,
∴△BCP是等腰三角形,
如图1,连接AP,
∵O为斜边中点,OP=OA,
∴BO=OP=OA,
∴∠APB=90°,
当BC=BP时,
∴∠BCP=∠BPC,
∴∠BCP+∠ACP=∠BPC+∠APC=90°,
∴∠ACP=∠APC,
∴AC=AP,
∴AB垂直平分PC,
∴∠ABP=∠ABC=25°,
∴θ=2×25°=50°,
当BC=PC时,如图2,连接CO并延长交PB于H,
∵BC=CP,BO=PO,
∴CH垂直平分PB,
∴∠CHB=90°,
∵OB=OC,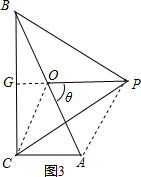
∴∠BCH=∠ABC=25°,
∴∠CBH=65°,
∴∠OBH=40°,
∴θ=2×40°=80°,
当PB=PC时,如图3,
连接PO并延长交BC于G,连接OC,
∵∠ACB=90°,O为斜边中点,
∴OB=OC,
∴PG垂直平分BC,
∴∠BGO=90°,
∵∠ABC=25°,
∴θ=∠BOG=65°,
综上所述:当△BCP恰为轴对称图形时,θ的值为50°或65°或80°,
故答案为:50°或65°或80°.
 ∵△BCP恰为轴对称图形,
∵△BCP恰为轴对称图形,∴△BCP是等腰三角形,
如图1,连接AP,
∵O为斜边中点,OP=OA,
∴BO=OP=OA,
∴∠APB=90°,
当BC=BP时,
∴∠BCP=∠BPC,
∴∠BCP+∠ACP=∠BPC+∠APC=90°,

∴∠ACP=∠APC,
∴AC=AP,
∴AB垂直平分PC,
∴∠ABP=∠ABC=25°,
∴θ=2×25°=50°,
当BC=PC时,如图2,连接CO并延长交PB于H,
∵BC=CP,BO=PO,
∴CH垂直平分PB,
∴∠CHB=90°,
∵OB=OC,

∴∠BCH=∠ABC=25°,
∴∠CBH=65°,
∴∠OBH=40°,
∴θ=2×40°=80°,
当PB=PC时,如图3,
连接PO并延长交BC于G,连接OC,
∵∠ACB=90°,O为斜边中点,
∴OB=OC,
∴PG垂直平分BC,
∴∠BGO=90°,
∵∠ABC=25°,
∴θ=∠BOG=65°,
综上所述:当△BCP恰为轴对称图形时,θ的值为50°或65°或80°,
故答案为:50°或65°或80°.
看了 如图在Rt△ACB中,C为直...的网友还看了以下:
如图,直角坐标系中,A,B两点的坐标分别为(8,0)和(0,6),点C为AB的中点,点D在x轴上,当 2020-03-30 …
如图,在△ABC中,∠C=90°,AC=4,BC=2,点A,C分别在X轴和Y轴上,当点A在X轴上运 2020-06-03 …
(2013•南沙区一模)将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点 2020-07-08 …
在直角坐标系中三角形ABC满足:角C=90°AC=2BC=1点AC分别在x轴y轴上当点A从原点开始 2020-07-24 …
(人教版)已知平面直角坐标系中,B(-3,0),A为y轴正半轴上一动点,半径为52的⊙A交y轴于点 2020-07-29 …
在平面直角坐标系中,点C的坐标为(2,2),将直角三角尺绕直角顶点C进行旋转,两条直角边分别与x轴 2020-07-30 …
如图△ABO为边长为2的等边三角形,P为x轴上一动点,以AP为一边作等边三角形△APQ。(1)如图① 2020-11-03 …
点P是x轴正半轴上的一个动点,过点P作x轴的垂线PA交双曲线y=1x于点A,连接OA并延长,与双曲线 2020-12-03 …
如图1,点A在y轴的正半轴上,以OA为边作等边三角形AOC.(1)点B是x轴正半轴上的一个动点,如图 2020-12-25 …
多用电表表头的示意图如图.①当档位选择开关和指针位置如图所示,则测量的物理量是,测量结果为.②若档位 2021-01-01 …