早教吧作业答案频道 -->数学-->
在平面直角坐标系中,点C的坐标为(2,2),将直角三角尺绕直角顶点C进行旋转,两条直角边分别与x轴正半轴,y轴交于点A,点B.(1)如图,当B与O重合时,试说明:AC=BC;(2)在旋转过
题目详情
在平面直角坐标系中,点C的坐标为(2,2),将直角三角尺绕直角顶点C进行旋转,两条直角边分别与x轴正半轴,y轴交于点A,点B.
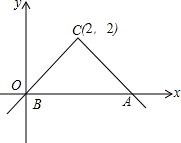
(1)如图,当B与O重合时,试说明:AC=BC;
(2)在旋转过程中,AC=BC这个结论还成立吗?请说明理由;
(3)在旋转的过程中,设A(a,0),B(0,b),请用含a的代数式表示b.

(1)如图,当B与O重合时,试说明:AC=BC;
(2)在旋转过程中,AC=BC这个结论还成立吗?请说明理由;
(3)在旋转的过程中,设A(a,0),B(0,b),请用含a的代数式表示b.
▼优质解答
答案和解析
(1)如图1,过点C作CD⊥x轴于点D,
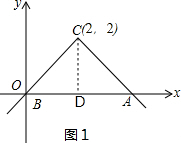
由题意可知AD=BD=2,
∴∠CBD=∠BCD=45°,
∵∠BCA=90°,
∴∠CAB=45°,
∴∠CBD=∠CAB=45°,
∴CB=CA;
(2)如图2,当点B在y轴正半轴上时,过点C作CD⊥x轴于点D,CE⊥y轴于点E,
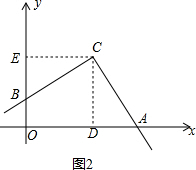
∴∠BOD=∠CDO=∠CEO=90°,
又∵CD=OD=2,
∴四边形ODCE为正方形,
∴CE=CD,
∵∠BCE+∠BCD=∠ACD+∠BCD=90°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
∵
,
∴△BCE≌△ACD(ASA),
∴AC=BC;
(3)由(2)知,AD=BE,即a-2=2-b,
∴b=4-a.

由题意可知AD=BD=2,
∴∠CBD=∠BCD=45°,
∵∠BCA=90°,
∴∠CAB=45°,
∴∠CBD=∠CAB=45°,
∴CB=CA;
(2)如图2,当点B在y轴正半轴上时,过点C作CD⊥x轴于点D,CE⊥y轴于点E,

∴∠BOD=∠CDO=∠CEO=90°,
又∵CD=OD=2,
∴四边形ODCE为正方形,
∴CE=CD,
∵∠BCE+∠BCD=∠ACD+∠BCD=90°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
∵
|
∴△BCE≌△ACD(ASA),
∴AC=BC;
(3)由(2)知,AD=BE,即a-2=2-b,
∴b=4-a.
看了 在平面直角坐标系中,点C的坐...的网友还看了以下:
抛物线y=-x2+2x+3与x轴相交于a,b两点,点a在b的左边,与y轴相交于点c,抛物线顶点为d 2020-05-16 …
请教一道数学题:已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos2 2020-05-16 …
在孔与轴的配合中,孔的尺寸减去与之相配合轴的尺寸,其差值为正时的配合被称为( )。A.过渡 2020-05-18 …
(2007•大连)如图1,直线y=-x+1与x轴、y轴分别相交于点C、D,一个含45°角的直角三角 2020-06-29 …
已知抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C已知抛 2020-07-20 …
角α的顶点在坐标原点O,始边在y轴的正半轴上,终边与单位圆交于第三象限内的点P,且tanα=-34 2020-07-30 …
1已知角a的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,问cos2a=?cosa 2020-07-30 …
已知抛物线y=ax2-2ax-3a与x轴交与A、B两点,与y轴负方向交与C点,且tan∠ACO=1 2020-07-31 …
打磨某剖面如图所示的宝石时,必须将OP、OQ边与轴线的夹角θ切割在θ1<θ<θ2的范围内,才能使从M 2020-10-30 …
如图,一个二次函数的图像与x轴交于A,B两点(A在B的左边),与y轴交于点c,起顶点坐标(-1,-8 2021-01-10 …