早教吧作业答案频道 -->数学-->
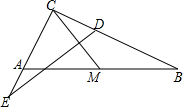
如图,点M是Rt△ABC的斜边AB的中点,连接CM,作线段CM的垂直平分线,分别交边CB和CA的延长线于点D、E,若∠C=90°,AB=20,tanB=25,则DE=.
题目详情
如图,点M是Rt△ABC的斜边AB的中点,连接CM,作线段CM的垂直平分线,分别交边CB和CA的延长线于点D、E,若∠C=90°,AB=20,tanB=
,则DE=___.
| 2 |
| 5 |

▼优质解答
答案和解析
∵∠C=90°,tanB=
,
设AC=2k,BC=5k,
∴AB=
=
k=20,
∴k=
,
∴BC=
,
连接DM,
∵∠C=90°,点M是Rt△ABC的斜边AB的中点,
∴AM=CM=BM
AB=10,
∴∠MCB=∠B,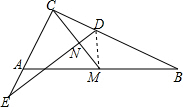
∵DE是线段CM的垂直平分线,
∴CD=DM,
∴∠DCM=∠DMC,
∴△CDM∽△CMB,
∴
=
,
∴CD=
,
∵DE垂直平分CM,
∴∠E+∠ECN=∠ECN+∠NCD=90°,
∴∠E=∠NCD,
∴△CDE∽△CDN,
∴
=
,
∵DN=
=2,
∴DE=
=
.
故答案为:
.
| 2 |
| 5 |
设AC=2k,BC=5k,
∴AB=
| AC2+BC2 |
| 29 |
∴k=
| 20 | ||
|
∴BC=
| 100 | ||
|
连接DM,
∵∠C=90°,点M是Rt△ABC的斜边AB的中点,
∴AM=CM=BM
| 1 |
| 2 |
∴∠MCB=∠B,

∵DE是线段CM的垂直平分线,
∴CD=DM,
∴∠DCM=∠DMC,
∴△CDM∽△CMB,
∴
| CM |
| BC |
| CD |
| CM |
∴CD=
| 29 |
∵DE垂直平分CM,
∴∠E+∠ECN=∠ECN+∠NCD=90°,
∴∠E=∠NCD,
∴△CDE∽△CDN,
∴
| CD |
| DE |
| DN |
| CD |
∵DN=
| CD2-CN2 |
∴DE=
| CD2 |
| DN |
| 29 |
| 2 |
故答案为:
| 29 |
| 2 |
看了 如图,点M是Rt△ABC的斜...的网友还看了以下:
PV/T=mR/M,PV/T=mr,r=R/M理想空气中这个r等于多少,M怎么计算. 2020-03-30 …
关于线代的问题.晕了,速32.非齐次线性方程组AX=b中未知数的个数为n,方程个数为m,系数矩阵A 2020-05-14 …
M、R都是生活中常见的金属单质,其中R是用量最多的金属.甲、乙是化合物,其中甲是黑色晶体,可由R在 2020-06-06 …
汇编中,ModR/M里,R/M具体含义是什么?ModR/M决定操作数的过程中,这个R/M到底表示什 2020-06-08 …
请教高手给出概率解释(大三以上的进)C(m,k)*C(n-m,r-k)/C(n,r)=C(r,k) 2020-06-11 …
已知集合A={x|x²-2x-3≤0,x∈R},B{x|x²-2mx+m²-4≤0,x∈R,m∈R 2020-06-12 …
(2010•福建模拟)考察等式:C0mCrn−m+C1mCr−1n−m+…+CrmC0n−m=Cr 2020-07-09 …
考察等式:C0mCrn-m+C1mCr-1n-m+…+CrmC0n-m=Crn(*),其中n、m、 2020-07-09 …
已知α,β,r是三个平面,m,n,l是三条直线,则能得出m⊥β的一个条件是Aα⊥β,α∩β=l,m 2020-07-13 …
设b-a=r-b=兀/3,求tanatanb+tanbtanr+tanrtanab-a=r-b=兀 2020-07-13 …