早教吧作业答案频道 -->数学-->
求满足下列条件的椭圆的标准方程.(1)已知椭圆的焦点在X轴上,长轴长是短轴长的3倍,且过点A(3,0).(2)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点,.
题目详情
求满足下列条件的椭圆的标准方程.
(1)已知椭圆的焦点在X轴上,长轴长是短轴长的3倍,且过点A(3,0).
(2)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点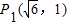 ,
,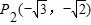 .
.
(1)已知椭圆的焦点在X轴上,长轴长是短轴长的3倍,且过点A(3,0).
(2)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点
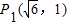 ,
,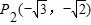 .
.▼优质解答
答案和解析
分析:
(1)根据题意得椭圆的长半轴a=3,且短半轴b=a,由此不难得到椭圆的方程;(2)设椭圆方程为mx2+ny2=1(m、n是不相等的正数),代入P1、P2两点的坐标,解出m、n的值即可得到椭圆的方程.
(1)∵椭圆的焦点在x轴上,∴设椭圆方程为(a>b>0)∵椭圆经过点A(3,0),且长轴长是短轴长的3倍,∴a=3b,且a=3,可得a=3,b=1,可得椭圆方程为;(2)设椭圆方程为mx2+ny2=1(m、n是不相等的正数)∵,在椭圆上,∴点的坐标代入,得,解之得,可得椭圆方程为,即.故所求椭圆方程为.
点评:
本题给出椭圆的满足的条件,求椭圆的标准方程,着重考查了利用待定系数法求椭圆的标准方程的方法,属于基础题.
分析:
(1)根据题意得椭圆的长半轴a=3,且短半轴b=a,由此不难得到椭圆的方程;(2)设椭圆方程为mx2+ny2=1(m、n是不相等的正数),代入P1、P2两点的坐标,解出m、n的值即可得到椭圆的方程.
(1)∵椭圆的焦点在x轴上,∴设椭圆方程为(a>b>0)∵椭圆经过点A(3,0),且长轴长是短轴长的3倍,∴a=3b,且a=3,可得a=3,b=1,可得椭圆方程为;(2)设椭圆方程为mx2+ny2=1(m、n是不相等的正数)∵,在椭圆上,∴点的坐标代入,得,解之得,可得椭圆方程为,即.故所求椭圆方程为.
点评:
本题给出椭圆的满足的条件,求椭圆的标准方程,着重考查了利用待定系数法求椭圆的标准方程的方法,属于基础题.
看了 求满足下列条件的椭圆的标准方...的网友还看了以下:
利用水煤气制取合成天然气的反应在523K是的标准平衡常数KC0(g)+3H2(g)==CH4(g) 2020-04-07 …
已知椭圆的中心在原点焦点坐标为(-根号3,0),(根号3,0),焦点构成一个正三角形,求椭圆的标准 2020-05-13 …
国际上再保险合同中应用较为普遍的仲裁条款是( )的"标准合同条款"。 A.美国B.法国C. 2020-05-21 …
国际上再保险合同中应用较为普遍的仲裁条款是( )的"标准合同条款"。A.美国B.法国###SX 2020-05-22 …
国际上再保险合同中应用较为普遍的仲裁条款是( )的“标准合同条款”。A.美国B.法国###SXB 2020-05-22 …
国际上再保险合同中应用较为普遍的仲裁条款是( )的标准合同条款。 2020-05-22 …
国际上再保险合同中应用较为普遍的仲裁条款是( )的"标准合同条款"。A.美国B.法国C.英国D.中国 2020-05-22 …
已知椭圆的对称轴是坐标轴,以短轴的一个端点和两焦点为顶点的三角形是正三角行,且焦点到椭圆的最短距离 2020-06-03 …
据抛物线y=ax^2-1的焦点坐标为坐标原点,为什么可以得出焦点坐标为(0,(1/4a)-1),我 2020-06-04 …
下列实轴长、虚轴长、焦距、焦点坐标、顶点坐标、离心率和渐近线方程(1)x^2-8y^2=32(2) 2020-06-14 …