早教吧作业答案频道 -->数学-->
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.(1)求证:MN⊥平面A1BC;(2)求直线BC1和平面A1BC所成角的大小;(3)求二面角A-BC-A1的平面的余弦值;(4)求点B
题目详情
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.
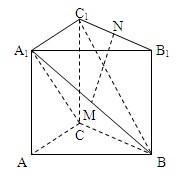
(1)求证:MN⊥平面A1BC;
(2)求直线BC1和平面A1BC所成角的大小;
(3)求二面角A-BC-A1的平面的余弦值;
(4)求点B1到平面A1BC的距离.

(1)求证:MN⊥平面A1BC;
(2)求直线BC1和平面A1BC所成角的大小;
(3)求二面角A-BC-A1的平面的余弦值;
(4)求点B1到平面A1BC的距离.
▼优质解答
答案和解析
(1)证明:由已知BC⊥AC,BC⊥CC1,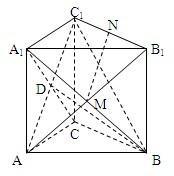
所以BC⊥平面ACC1A1.连接AC1,则BC⊥AC1.
由已知,侧面ACC1A1是矩形,所以A1C⊥AC1.
又BC∩A1C=C,所以AC1⊥平面A1BC.
因为侧面ABB1A1是正方形,M是A1B的中点,连接AB1,则点M是AB1的中点.
又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1.
故MN⊥平面A1BC.
(2) 因为AC1⊥平面A1BC,设AC1与A1C相交于点D,
连接BD,则∠C1BD为直线BC1和平面A1BC所成角.
设AC=BC=CC1=a,则C1D=
a,BC1=
a.
在Rt△BDC1中,sin∠C1BD=
,
所以∠C1BD=30°,故直线BC1和平面A1BC所成的角为30°.
(3) 由题意,∠A1CA为二面角A-BC-A1的平面角,
由于AC=BC=CC1=a,∴cos∠A1CA=
,
∴二面角A-BC-A1的平面角的余弦值为
;
(4) 设点B1到平面A1BC的距离为h,则由等体积可得
×
a•
a•h=
×
a•
a•
a,
∴h=
a.

所以BC⊥平面ACC1A1.连接AC1,则BC⊥AC1.
由已知,侧面ACC1A1是矩形,所以A1C⊥AC1.
又BC∩A1C=C,所以AC1⊥平面A1BC.
因为侧面ABB1A1是正方形,M是A1B的中点,连接AB1,则点M是AB1的中点.
又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1.
故MN⊥平面A1BC.
(2) 因为AC1⊥平面A1BC,设AC1与A1C相交于点D,
连接BD,则∠C1BD为直线BC1和平面A1BC所成角.
设AC=BC=CC1=a,则C1D=
| ||
| 2 |
| 2 |
在Rt△BDC1中,sin∠C1BD=
| 1 |
| 2 |
所以∠C1BD=30°,故直线BC1和平面A1BC所成的角为30°.
(3) 由题意,∠A1CA为二面角A-BC-A1的平面角,
由于AC=BC=CC1=a,∴cos∠A1CA=
| ||
| 2 |
∴二面角A-BC-A1的平面角的余弦值为
| ||
| 2 |
(4) 设点B1到平面A1BC的距离为h,则由等体积可得
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
∴h=
| ||
| 2 |
看了 如图,在直三棱柱ABC-A1...的网友还看了以下:
先能明白(1)小题的解答过程,再解答第(2)小题,(1)已知a²-3a+1=0,求a²+1/a²的值 2020-03-31 …
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
已知a大于0,b大于0,a+b=1,求证(a+1/a)(b+1/b)大于或等于25/4.解法里面有 2020-05-15 …
已知数列{a(n)}中,a(1)=2,a(n)-a(n-1)-2n=0(n≥2,n∈N),设Bn= 2020-05-21 …
已知f(X)=Lg1-X/1+X,a,b属于(-1,1)求证:f(a)+f(B)=F(A+B)/1 2020-05-22 …
(a+1)(a^2+1)(a^4+1)(a^8+1)(a^16+1)=(a-1)[(a+1)(a^ 2020-05-22 …
已知a/(a^2+1)=1/2,求a^2/(a^4+1)的值由a/(a^2+1)=1/2,知a≠0 2020-06-14 …
若关于x的方程x+2/x=c+2/c的解是x1=c,x2=2/c,则关于x的方程x+2/(x-1) 2020-06-27 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
已知a>0,b>0且a+b=1,则(1/a^2-1)(1/b^2-1)的最小值是多少?(1/a²-1 2020-11-01 …