早教吧作业答案频道 -->数学-->
已知函数.(1)证明:f(x)必有两个极值点;(2)设x1,x2是f(x)两个极值点且|x1|+|x2|=2,求a的取值范围并求b的最大值;(3)当a=3,b=4时,数列{an}满足:a1=e-1(e为自然对数的底数)
题目详情
已知函数 .
.
(1)证明:f(x)必有两个极值点;
(2)设x1,x2是f(x)两个极值点且|x1|+|x2|=2,求a的取值范围并求b的最大值;
(3)当a=3,b=4时,数列{an}满足:a1=e-1(e为自然对数的底数)且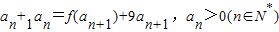 ,求证:
,求证: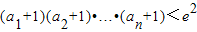 .
.
 .
.(1)证明:f(x)必有两个极值点;
(2)设x1,x2是f(x)两个极值点且|x1|+|x2|=2,求a的取值范围并求b的最大值;
(3)当a=3,b=4时,数列{an}满足:a1=e-1(e为自然对数的底数)且
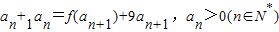 ,求证:
,求证: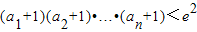 .
.▼优质解答
答案和解析
【答案】分析:(1)因为函数.对其进行求导,只要证明f′(x)=0,有两个根即可;(2)由(1)利用韦达定理得到两个根的关系,根据|x1|+|x2|=|x1-x2|,代入得到b与a的关系,可以令b2=g(a)利用导数研究g(a)的最值问题;(3)a=3,b=4时,代入f(x),由已知可得an+1an=+2,且an+1≠0,可以推出∴{ln(an+1)}是首项为1,公比为的等比数列,求出an的通项,从而求解;(1)因为函数.∴f′(x)=ax2+bx-a2,∵,∴△>0,即f′(x)=0必有两个根,设为x1,x2,且x1<x2,故有,若f′(x)>0,可得x<x1或x>x2,f(x)为增函数;若f′(x)<0,可得x1<x<x2,f(x)为减函数;所以f(x)必有两个极值点;(2)由(1)知,∴|x1|+|x2|=|x1-x2|===2,∴b2=4a2-4a3,∴⇒0<a≤1,设b2=g(a)=4a2-4a3,a∈(0,1],g′(a)=8a-12a2=4a(2-3a),由g′(a)>0,0<a<,由g′(a)<0,可得<a≤1,∴g(a)max=g()=,∴b2≤即|b|≤即bmin=;(3)由已知得:an+1an=+2,且an+1≠0,∴an=+2an+1⇒an+1=(an+1+1)2,又an+1>0,所以ln(an+1+1)=ln(an+1),ln(a1+1)=1,∴{ln(an+1)}是首项为1,公比为的等比数列,故ln(an+1)=()n-1,∴an+1=,(a1+1)(a2+1)…(an+1)==<e2;点评:利用导数求函数的极值问题,要注意极值点处的导数为0推出函数有极值;利用导数判断函数的单调区间,导函数大于0求出单调递增区间,导数小于0是递减区间,第三问难度比较大,需要用到前一题的结论进行证明,是一道综合性比较强的题;
看了 已知函数.(1)证明:f(x...的网友还看了以下:
f(x)=(x^3+bx^2+cx+d)e^x且f(0)=4-5b,x=1时有极值g(x)-x^2 2020-04-26 …
实数X,Y满足X方+Y方-2X+4Y=0求X方+Y方的范围;求X-1分之Y-1的范围;若X-2Y+ 2020-04-27 …
设函数f(x)=e^x-e^-x若对所有x≥0都有f(x)≥ax求a的范围e^x表示e的x次方,这 2020-06-03 …
求第三范式问题已知关系r(R)=r(A,B,C,D,E),且存在函数依赖集F=(AB→C,B→D, 2020-06-04 …
已知椭圆E的两个焦点分别为(-1,0)和(1,0),离心率e=2分之根号2求椭圆的方程若直线y=k 2020-07-31 …
如何一眼看出求参数范围的导数高考题是否可以用分离变量法1、大部分求参数范围高考题分离变量后会出现0 2020-07-31 …
方程组y^2=4x,y=2x+n有2组不同实数解.(1)求n的范围(2)若n在取值范围内,取最大整 2020-08-01 …
导数题已知函数f(x)=(x^2+mx+5)e^x,x属于全体实数.1.若函数没有极值点,求m的范围 2020-11-17 …
用C++求不超过30000E数列的最大E数的值/*数列:E(1)=E(2)=1E(n)=(n-1)* 2020-11-20 …
求答.十万火急已知函数f(x)=x/Inx.(1)求函数f(x)的单调减区间和极值;(2)当时x>1 2020-12-07 …