早教吧作业答案频道 -->数学-->
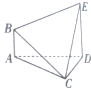
在如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AD=2,∠ACD=90°.求多面体ABEDC的体积.
题目详情
在如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AD=2,∠ACD=90°.求多面体ABEDC的体积.

▼优质解答
答案和解析
∵AB⊥平面ACD,DE⊥平面ACD,
且AC=CD,DE=2AB=2,AD=2,∠ACD=90°,
∴AC=CD=
,点C到平面ABED的距离h=1,
∵S四边形ABED=
(1+2)×2=3,
∴多面体ABEDC的体积V=
S四边形ABED•h=
×3×
=
.

且AC=CD,DE=2AB=2,AD=2,∠ACD=90°,
∴AC=CD=
| 2 |
∵S四边形ABED=
| 1 |
| 2 |
∴多面体ABEDC的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 2 |
看了 在如图所示的多面体ABEDC...的网友还看了以下:
在三角形ABC中,角A,B,C所对的边分别为a,b,c,若a+b=c(cosA+cosB)(1)判 2020-04-07 …
如图所示,在光滑水平桌面上放有长木板C,在C上左端和距左端x处各放有小物块A和B,A、B的体积大小 2020-05-17 …
八下勾股定理在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C所对的边(1)若a=5.b 2020-06-06 …
20℃时,配制一组c(Na2CO3)+c(NaHCO3)=0.100mol·L-1的混合溶液,溶液 2020-06-12 …
求解Orz在三角形ABC中,内角A、B、C所对的边分别为a,b,c,已知a-c=根号6/6,sin 2020-06-17 …
在三角形ABC中,内角A、B、C所对边长分别为a、b、c,求证:a^2=b^2+c^2-2向量AB 2020-07-13 …
已知三角形ABC的内角A,B,C所对应的边分别为a,b,c.且a=1,cosB=3/5(...已知 2020-07-13 …
已知扇形的圆心角是α,所在圆的半径是R,若扇形的周长是一定值C(C>0)当α为多少弧度时,该扇形的 2020-07-26 …
(1)用坐标法证明余弦定理:已知在△ABC中,角A、B、C所对的边分别为a、b、c,求证:a2=b 2020-07-29 …
已知abc分别为三角形ABC三个角A,B,C所对应的边,且有如下关系式:a/cos二分之角A=b/c 2020-12-07 …