早教吧作业答案频道 -->数学-->
如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.(1)求证:△CAE∽△CBF;(2)若BE=1,AE=2,求CE的长.
题目详情
如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.
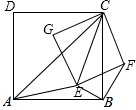
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.

(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD和EFCG均为正方形,
∴
=
=
,
∴∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF.
(2) ∵△CAE∽△CBF,
∴∠CAE=∠△CBF,
=
,
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵
=
=
,AE=2
∴
=
,
∴BF=
,
∴EF2=BE2+BF2=3,
∴EF=
,
∵CE2=2EF2=6,
∴CE=
.
∴
| AC |
| BC |
| CE |
| CF |
| 2 |
∴∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF.
(2) ∵△CAE∽△CBF,
∴∠CAE=∠△CBF,
| AE |
| BF |
| AC |
| BC |
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵
| AE |
| BF |
| AC |
| BC |
| 2 |
∴
| 2 |
| BF |
| 2 |
∴BF=
| 2 |
∴EF2=BE2+BF2=3,
∴EF=
| 3 |
∵CE2=2EF2=6,
∴CE=
| 6 |
看了 如图,已知AC,EC分别为正...的网友还看了以下:
已知函数f(x)=-x^3+ax^2+bx+c图像上的点p(1.f(1))处的切线方程为y=_3x 2020-04-05 …
f(x)=x^3+bx^2+cx有两个不同的极值点A,B.设f(x)在点(1,f(1))和(-1, 2020-04-26 …
已知函数f(x)=alnx/(x+1) + b/x ,曲线y=f(x)在点(1,f(1))处切线方 2020-05-15 …
已知函数f(x)=alnx/(x+1)+b/x,曲线y=f(x)在点(1,f(1))处的切线方程为 2020-05-17 …
已知函数f(x)=alnxx+1+bx,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y 2020-06-03 …
已知函数f(x)=2/x+alnx-2(1)若函数y=f(x)在点P(1,f(1))处的切线与直线 2020-06-08 …
设f(x)是偶函数.若曲线y=f(x)在点(1,f(1))处的切线的斜率为1,则:设f(x)是偶函 2020-07-08 …
高中数学(切线、函数)函数f(x)=ax^3+bx+c(a0)为奇函数,其图像在点(1,f(1)) 2020-07-09 …
函数f(x)的倒数1/f(x)表示成-1次方怎么写,书上f(x)的2次方是f^2(x),但是f^- 2020-08-01 …
已知函数f(x)当x>0时满足f''(x)+3[f'(x)]^2=xlnx且f'(1)=0,则(C) 2021-02-01 …