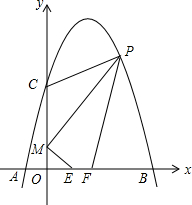
如图，对称轴为直线x=2的抛物线经过点A（-1，0），C（0，5）两点，与x轴另一交点为B，已知M（0，1），E（a，0），F（a+1，0），点P是第一象限内的抛物线上的动点．（1）求此抛物线的解析

Question

如图，对称轴为直线x=2的抛物线经过点A（-1，0），C（0，5）两点，与x轴另一交点为B，已知M（0，1），E（a，0），F（a+1，0），点P是第一象限内的抛物线上的动点．

（1）求此抛物线的解析式；
（2）当a=1时，求四边形MEFP面积的最大值，并求此时点P的坐标．

Answer 1

（1）∵对称轴为直线x=2，
∴设抛物线解析式为y=a（x-2）²+k．
将A（-1，0），C（0，5）代入得：

9a+k=0

4a+k=5

，
解得

a=-1

k=9

，
∴y=-（x-2）²+9=-x²+4x+5．

（2）当a=1时，E（1，0），F（2，0），OE=1，OF=2．
设P（x，-x²+4x+5），
如答图2，过点P作PN⊥y轴于点N，则PN=x，ON=-x²+4x+5，
∴MN=ON-OM=-x²+4x+4．

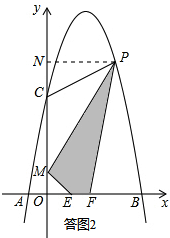
S_{四边形MEFP}=S_梯形OFPN-S_△PMN-S_△OME
=(1)/(2)（PN+OF）•ON-(1)/(2)PN•MN-(1)/(2)OM•OE
=(1)/(2)（x+2）（-x²+4x+5）-(1)/(2)x•（-x²+4x+4）-(1)/(2)×1×1
=-x²+(9)/(2)x+(9)/(2)
=-（x-(9)/(4)）²+(153)/(16)，
∴当x=(9)/(4)时，四边形MEFP的面积有最大值为(153)/(16)，
把x=(9)/(4)时，y=-（(9)/(4)-2）²+9=(143)/(16)．
此时点P坐标为（(9)/(4)，(143)/(16)）．