早教吧作业答案频道 -->数学-->
已知y=ax2+bx+c(a<0),图象过点(-1,0),对称轴为x=2,有下列结论:(1)4a+b=0;(2)c+9a>3b;(3)8a+7b+2c<0.正确结论有几个?
题目详情
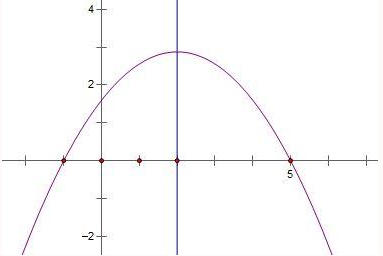 已知y=ax 2 +bx+c(a<0),图象过点(-1,0),对称轴为x=2,有下列结论:
已知y=ax 2 +bx+c(a<0),图象过点(-1,0),对称轴为x=2,有下列结论:(1)4a+b=0;(2)c+9a>3b;(3)8a+7b+2c<0.
正确结论有几个?
▼优质解答
答案和解析
考点:
二次函数图象与系数的关系
专题:
分析:
(1)利用抛物线的对称轴即可判定;(2)把x=-3时代入即可判定;(3)由抛物线与x的交点为(-1,0),可得a-b+c=0,由b=-4a,可得c=-5a,化简8a+7b+2c=8a-28a-10a=-30a,由a<0,即可得8a+7b+2c>0.
(1)∵抛物线的对称轴为x=-b2a=2,∴b=-4a,即4a+b=0,所以①正确.(2)∵当x=-3时,y<0,∴9a-3b+c<0,即c+9a<3b.∴②错误.(3)∵抛物线与x的交点为(-1,0),∴a-b+c=0,∵b=-4a,a+4a+c=0,即c=-5a,∴8a+7b+2c=8a-28a-10a=-30a,∵a<0,∴8a+7b+2c>0. ∴③错误.所以正确的有1个.
点评:
本题主要考查了二次函数图象与系数关系,解题的关键是利用对称轴求出a,b的关系.
考点:
二次函数图象与系数的关系
专题:
分析:
(1)利用抛物线的对称轴即可判定;(2)把x=-3时代入即可判定;(3)由抛物线与x的交点为(-1,0),可得a-b+c=0,由b=-4a,可得c=-5a,化简8a+7b+2c=8a-28a-10a=-30a,由a<0,即可得8a+7b+2c>0.
(1)∵抛物线的对称轴为x=-b2a=2,∴b=-4a,即4a+b=0,所以①正确.(2)∵当x=-3时,y<0,∴9a-3b+c<0,即c+9a<3b.∴②错误.(3)∵抛物线与x的交点为(-1,0),∴a-b+c=0,∵b=-4a,a+4a+c=0,即c=-5a,∴8a+7b+2c=8a-28a-10a=-30a,∵a<0,∴8a+7b+2c>0. ∴③错误.所以正确的有1个.
点评:
本题主要考查了二次函数图象与系数关系,解题的关键是利用对称轴求出a,b的关系.
看了 已知y=ax2+bx+c(a...的网友还看了以下:
已知:实数a,b,c在数轴上的位置如图所示,且,a的绝对值=b的绝对值.化简:a的绝对值+a和b的 2020-04-05 …
已知实数a,b,c在数轴上的位置如图所示,且绝对值a=绝对值b化简绝对值a加绝对值a加b-根号c- 2020-04-06 …
如图,对称轴为直线x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,去当△ac 2020-05-15 …
那重庆2013中考数学(A卷)的25题呢?如图,对称轴为直线x=-1的抛物线y=ax2+bx+c( 2020-05-15 …
已知二次函数y=x的平方+(a-b)x+b图像如图,化简:分子是:根号下a的平方-2ab+b的平方 2020-05-16 …
已知二次函数f(x)=ax^2+bx+c的导数为f'(x),f'(x)>0.对任意实数x,有f(x 2020-05-17 …
已知函数f(x)=asin(wxa)平房(a大于0,w大于0,a大于0小于派/2),且y=f(x) 2020-06-02 …
二次函数y=ax2+k的图象如图所示,则对应a,k的符号正确的是()A、a>0,k>0B、a>0,k 2020-11-01 …
函数图像的平移与对称题若y=log以a为底x的对数与y=log以b为底x的对数(a>0,b>0且a不 2020-12-12 …
已知二次函数图象过A(-1,0),C(0,3)且对称轴为直线x=1.(1)求抛物线的解析式,图象与x 2021-02-05 …