早教吧作业答案频道 -->数学-->
二次函数y=ax2+k的图象如图所示,则对应a,k的符号正确的是()A、a>0,k>0B、a>0,k<0C、a<0,k>0D、a<0,k<0
题目详情
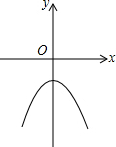 二次函数y=ax 2 +k的图象如图所示,则对应a,k的符号正确的是( )
二次函数y=ax 2 +k的图象如图所示,则对应a,k的符号正确的是( )| A、a>0,k>0 |
| B、a>0,k<0 |
| C、a<0,k>0 |
| D、a<0,k<0 |
▼优质解答
答案和解析
考点:
二次函数图象与系数的关系
专题:
分析:
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断k与0的关系.
∵抛物线y=ax2+k的开口向下,∴a<0,∵与y轴的交点在y轴的负半轴上,∴k<0.故选D.
点评:
本题考查二次函数图象与系数的关系,对于二次函数y=ax2+bx+c(a≠0)来说,①二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;|a|还可以决定开口大小,|a|越大开口就越小;②一次项系数b和二次项系数a共同决定对称轴的位置. 当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);③常数项c决定抛物线与y轴交点,抛物线与y轴交于(0,c).④抛物线与x轴交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
考点:
二次函数图象与系数的关系
专题:
分析:
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断k与0的关系.
∵抛物线y=ax2+k的开口向下,∴a<0,∵与y轴的交点在y轴的负半轴上,∴k<0.故选D.
点评:
本题考查二次函数图象与系数的关系,对于二次函数y=ax2+bx+c(a≠0)来说,①二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;|a|还可以决定开口大小,|a|越大开口就越小;②一次项系数b和二次项系数a共同决定对称轴的位置. 当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);③常数项c决定抛物线与y轴交点,抛物线与y轴交于(0,c).④抛物线与x轴交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
看了二次函数y=ax2+k的图象如...的网友还看了以下:
异步串行通信接口标准RS-232C的逻辑0的信号电平是( )。A.0~5VB.3~15VC.-15~ 2020-05-23 …
异步串行通信接口标准RS-232C的逻辑0的信号电平是( )。A.0~5VB.3~15VC.-15~ 2020-05-24 …
异步串行通信接口标准RS-232C的逻辑0的信号电平是( )。A.OV~+5VB.+3V~+15VC 2020-05-24 …
异步串行通信接口标准RS-232C的逻辑0的信号电平是( )。A.0V~+5VB.+3V~+15VC 2020-05-24 …
异步串行通信接口标准RS-232C的逻辑0的信号电平是( )。A.0~5VB.3~15VC.-15~ 2020-05-24 …
异步串行通信接口标准RS-232C的逻辑0的信号电平是( )。A.0V~+5VB.+3V~+15VC 2020-05-24 …
为什么a^2+b^2<1,表示半径为1的圆?这是某题答案,看不懂最后一句由题意得:抛物线y=x2+ 2020-06-07 …
用>号或<号填空①若m>0,n>0,则m+n0;②若m<0,n<0,则m+n0;③若m>0,n<0 2020-07-19 …
(1)比较下面各数并用小于号连接起来.0.95524259.5%0.979.5%<0.955<24 2020-08-01 …
12.如果a+b<0,且ab<0,则()A.a>0,b>0B.a<0,b<0C.a、b异号且负数的绝 2021-01-22 …