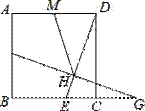
如图，边长为6的正方形ABCD中，点E是BC上一点，点F是AB上一点．点F关于直线DE的对称点G恰好在BC延长线上，FG交DE于点H．点M为AD的中点，若MH=，则EG．

Question

如图，边长为6的正方形ABCD中，点E是BC上一点，点F是AB上一点．点F关于直线DE的对称点G恰好在BC延长线上，FG交DE于点H．点M为AD的中点，若MH=，则EG　　．

Answer 1

【考点】相似三角形的判定与性质；正方形的性质．

【分析】连接DF，DG，过H作HP⊥AB于P，HQ⊥AD于Q，由点F，点G关于直线DE的对称，得到DF=DG，根据正方形的性质得到AD=CD，∠ADC=∠A=∠BCD=90°，推出Rt△AFD≌Rt△CDG，证得△FDG是等腰直角三角形，推出四边形APHQ是矩形，证得△HPF≌△DHQ，根据全等三角形的性质得到HP=HQ，推出△MHQ≌△DHQ，根据全等三角形的性质得到DH=MH=，DQ=QM=，求得CH=DH=，通过△DQH∽△CEH，根据相似三角形的性质即可得到结论．

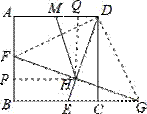
【解答】连接DF，DG，过H作HP⊥AB于P，HQ⊥AD于Q，

∵点F，点G关于直线DE的对称，

∴DF=DG，

正方形ABCD中，

∵AD=CD，∠ADC=∠A=∠BCD=90°，

∴∠GCD=90°，

在Rt△AFD与Rt△CDG中，，

∴Rt△AFD≌Rt△CDG，

∴∠ADF=∠CDG，

∴∠FDG=∠ADC=90°，

∴△FDG是等腰直角三角形，

∵DH⊥CF，

∴DH=FH=FG，

∵HP⊥AB，HQ⊥AD，∠A=90°，

∴四边形APHQ是矩形，

∴∠PHQ=90°，

∵∠DHF=90°，

∴∠PHF=∠DHQ，

在△PFF与△DQH中，，

∴△HPF≌△DHQ，

∴HP=HQ，

∵∠PHF=90°﹣∠FHM，∠QHM=90°﹣∠FHM，

∴∠PHF=∠QHM，

∴∠QHM=∠DHQ，

在△MHQ与△DHQ中，，

∴△MHQ≌△DHQ，

∴DH=MH=，DQ=QM=，

∴CH=DH=，

∵点M为AD的中点，

∴DM=3，∴DQ=QM=，

∴HQ==，

∵∠QDH=∠HEG，

∴△DQH∽△CEH，

∴，

即，

∴EG=．

故答案为：．